
题目列表(包括答案和解析)
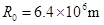 ;
;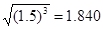 ;
;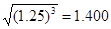
(1)开普勒从1609年~1619年发表了著名的开普勒行星运动三定律,其中第一定律为:所有的行星分别在大小不同的椭圆轨道上围绕太阳运动,太阳在这个椭圆的一个焦点上。第三定律:所有行星的椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等.实践证明,开普勒三定律也适用于其他中心天体的卫星运动。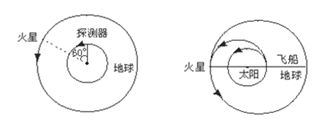
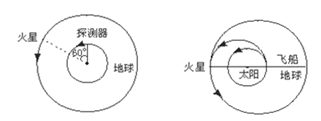
(2)从地球表面向火星发射火星探测器.设地球和火星都在同一平面上绕太阳做圆周运动,火星轨道半径Rm为地球轨道半径R0的1.5倍,简单而又比较节省能量的发射过程可分为两步进行:第一步,在地球表面用火箭对探测器进行加速,使之获得足够动能,从而脱离地球引力作用成为一个沿地球轨道运动的人造行星。第二步是在适当时刻点燃与探测器连在一起的火箭发动机,在短时间内对探测器沿原方向加速,使其速度数值增加到适当值,从而使得探测器沿着一个与地球轨道及火星轨道分别在长轴两端相切的半个椭圆轨道正好射到火星上.当探测器脱离地球并沿地球公转轨道稳定运行后,在某年3月1日零时测得探测器与火星之间的角距离为60°,如图所示,问应在何年何月何日点燃探测器上的火箭发动机方能使探测器恰好落在火星表面?(时间计算仅需精确到日),已知地球半径为: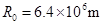 ;
;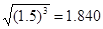 ;
;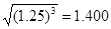
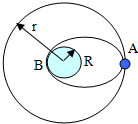 开普勒在1609-1619年发表了著名的开普勒行星三定律,其中第三定律的内容:所有行星在椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等.实践证明.开普勒三定律也适用于人造地球卫星.2005年10月17日,“神舟”六号飞船在绕地球飞行5天后顺利返回.“神舟”六号飞船在圆轨道正常运行时,其圆轨道半径为r,返回过程可简化为:圆轨道上飞船,在适当位置开动制动发动机一小段时间(计算时可当作一瞬时),使飞船速度减小,并由圆轨道转移到与地面相切的椭圆轨道上,如图所示,椭圆轨道与地面的切点即为设在内蒙的飞船主着陆场,设地球半径为R,地球表面的重力加速度为g,圆轨道为椭圆轨道的一种特殊情况,空气阻力不计.问:
开普勒在1609-1619年发表了著名的开普勒行星三定律,其中第三定律的内容:所有行星在椭圆轨道的半长轴的三次方跟公转周期的平方的比值都相等.实践证明.开普勒三定律也适用于人造地球卫星.2005年10月17日,“神舟”六号飞船在绕地球飞行5天后顺利返回.“神舟”六号飞船在圆轨道正常运行时,其圆轨道半径为r,返回过程可简化为:圆轨道上飞船,在适当位置开动制动发动机一小段时间(计算时可当作一瞬时),使飞船速度减小,并由圆轨道转移到与地面相切的椭圆轨道上,如图所示,椭圆轨道与地面的切点即为设在内蒙的飞船主着陆场,设地球半径为R,地球表面的重力加速度为g,圆轨道为椭圆轨道的一种特殊情况,空气阻力不计.问:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com