实验题（在用落体法“验证机械能守恒定律”的实验中，（设当地的重力加速度g为已知），
（1）带动纸带下落的重物有以下几种：
A．质量为1g的钩码B．质量为5g的塑料球
C．质量为200g的钩码D．质量为200g的软木块
其中最理想的重物是，理由是．
（2）某同学列举的实验步骤有以下几项：
A．用天平测量出重锤的质量
B．释放纸带时纸带应保持竖直
C．实验时应先接通电源再释放纸带
D．选取合格的打点纸带进行数据处理
其中没有必要的步骤是理由是．
（3）在“验证机械能守恒定律”的实验中，用质量m=0.50kg的重锤拖着纸带由静止开始下落，在下落过程中，打点计时器在纸带上打出一系列的点．在纸带上选取三个相邻的计数点D、E和F，相邻计数点间的时间间隔为T=0.1s．O为重锤开始下落时记录的点，各计数点到O点的距离如图所示，长度的单位是cm，当地的重力加速度g取10m/s²．
①打点计时器打下计数点E时，重锤下落的速度v_E= m/s；（结果保留两位有效数字）
②打点计时器从打下计数点O到打下计数点E的过程中，重锤动能的增加量△E_k=J，
重锤重力势能的减小量△E_p= J．（结果保留两位有效数字）

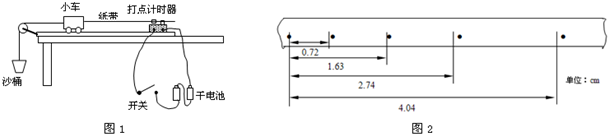
实验桌上有外形十分相似的发光二极管和电容器各一只，它们的性能均正常．
（1）现在用多用电表的欧姆挡，分别测量它们的正反向电阻．测量结果如下：测甲元件时，R_正=0.5kΩ，R_反=100kΩ；测乙元件时，开始时指针偏转到0.5kΩ，接着读数逐渐增加，最后停在“∞”上．则甲、乙二个元件分别是、．
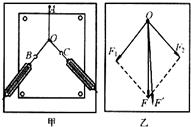
（2）若想测量上述发光二极管的发光效率，某同学设计了如图甲所示的实验：将一个标有“0.5V 1W”的发光二极管接入电路，使之正常发光，在发光二极管的同一水平面、正对光线方向放一个光强探头，以测定与光源间距为d时相应的光强值I（单位面积上光的照射功率）．实验测得数据如下表，并用一数字图象处理器将表内数据分别在I-d、I-d^-1、I-d^-2坐标平面内标得如下数据点，如图乙所示．

d/×10-2m	2.50	3.50	4.50	5.50	6.50	7.50	8.50	9.50
I/W?m-2	32.00	16.33	9.97	6.61	4.73	3.56	2.77	2.22

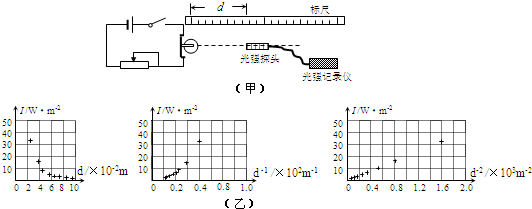
①根据图中三个数据点图，可以将I与d之间的数学关系式写为，其中的常量为．
②若把发光二极管看成点光源，在与点光源等距离的各点，可以认为光源向各个方向发出的光强大小几乎相等．此时，我们可以建立一个点光源散射光的模型，从而求出光源的发光功率P₀、光强I及相应的与光源距离d之间的关系式：P₀=．
③根据以上条件和有关数据，可以算出这个发光二极管的电--光转换效率约为η=．（不考虑光传播过程中的能量损失）

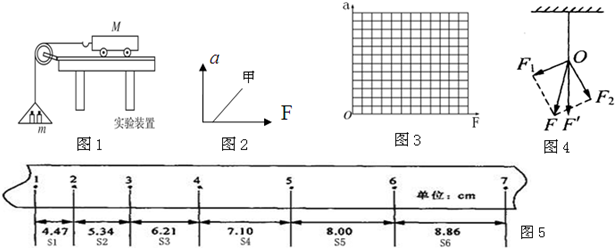
实验题（在用落体法“验证机械能守恒定律”的实验中，（设当地的重力加速度g为已知），
（1）带动纸带下落的重物有以下几种：
A．质量为1g的钩码B．质量为5g的塑料球
C．质量为200g的钩码D．质量为200g的软木块
其中最理想的重物是______，理由是______．
（2）某同学列举的实验步骤有以下几项：
A．用天平测量出重锤的质量
B．释放纸带时纸带应保持竖直
C．实验时应先接通电源再释放纸带
D．选取合格的打点纸带进行数据处理
其中没有必要的步骤是______理由是______．
（3）在“验证机械能守恒定律”的实验中，用质量m=0.50kg的重锤拖着纸带由静止开始下落，在下落过程中，打点计时器在纸带上打出一系列的点．在纸带上选取三个相邻的计数点D、E和F，相邻计数点间的时间间隔为T=0.1s．O为重锤开始下落时记录的点，各计数点到O点的距离如图所示，长度的单位是cm，当地的重力加速度g取10m/s²．
①打点计时器打下计数点E时，重锤下落的速度v_E=______ m/s；（结果保留两位有效数字）
②打点计时器从打下计数点O到打下计数点E的过程中，重锤动能的增加量△E_k=______J，
重锤重力势能的减小量△E_p=______ J．（结果保留两位有效数字）