阅读下面文言文,完成小题。
主父偃者,齐临淄人也。游齐诸生间,莫能厚遇也。
齐诸儒生相与排摈,不容于齐。家贫,假贷无所得,乃北游燕、赵、中山,皆莫能厚遇,为客甚困。孝武元光元年中,以为诸侯莫足游者,乃西入关见卫将军。卫将军数言上,上不召。资用乏,留久,诸公宾客多厌之,乃上书阙下。朝奏,暮召入见;拜为郎中。偃数见,上疏言事。诏拜偃为谒者,迁为中大夫。一岁中四迁偃。
偃说上曰:“古者诸侯不过百里,强弱之形易制。今诸侯或连城数十,地方千里,缓则骄奢易为淫乱,急则阻其强而合从以逆京师。今以法割削之,则逆节萌起,前日晁错是也。今诸侯子弟或十数,而嫡嗣代立,
余虽骨肉无尺寸地封则仁孝之道不宣愿陛下令诸侯得推恩分子弟以地侯之彼人人喜得所愿上以德施实分其国不削而稍弱矣于是上从其计。
尊立卫皇后,及发燕王定国阴事,盖偃有功焉。大臣皆畏其口,赂遗累千金。人或说偃曰:“太横矣。”主父曰:“臣结发游学四十余年,身不得遂,亲不以为子,昆弟不收,宾客弃我,我厄日久矣。且丈夫生不五鼎食①,死即五鼎烹②耳。吾日暮途远,故倒行暴施之。”
元朔二年,上拜主父为齐相。至齐,遍召昆弟宾客,散五百金予之,数之曰:“
始吾贫时,昆弟不我衣食,宾客不我内门;今吾相齐,诸君迎我或千里。吾与诸君绝矣,毋复入偃之门!”乃使人以王与姊奸事动王,王以为终不得脱罪,乃自杀。
主父始为布衣时,尝游燕、赵,及其贵,发燕事。赵王恐其为国患,欲上书言其阴事,为偃居中,不敢发。及为齐相,出关,即使人上书,告言主父偃受诸侯金,以故诸侯子弟多以得封者。及齐王自杀,上闻大怒,以为主父劫其王令自杀,乃遂族主父偃。
(选自《史记·平津侯主父列传》,有删改)
注:①五鼎食:牛、羊、豕、鱼、麋也。诸侯五,卿大夫三。②五鼎烹:被镬(一种大锅)烹煮的刑罚。
【小题1】对下列句子中加线的词语的解释,不正确的一项是( )(3分)
| A.家贫,假贷无所得假:借。 |
| B.古者诸侯不过百里过:经过。 |
| C.身不得遂,亲不以为子亲:父母。 |
| D.我厄日久矣厄:穷困。 |
【小题2】下列各组句子中,加线词的意义和用法都相同的一组是( )(3分)
| A.诸公宾客多厌之/强弱之形易制 |
| B.今以法割削之 /亲不以为子 |
| C.乃西入关见卫将军 / 王以为终不得脱罪,乃自杀 |
| D.急则阻其强而合从以逆京师 / 今诸侯子弟或十数,而嫡嗣代立 |
【小题3】下列句子分别编为四组,全都属于武帝“族偃”原因的一组是( )(3分)
①及发燕王定国阴事
②吾与诸君绝矣,毋复入偃之门
③乃使人以王与姊奸事动王,王以为终不得脱罪,乃自杀
④告言主父偃受诸侯金,以故诸侯子弟多以得封者
⑤上闻大怒,以为主父劫其王令自杀
【小题4】下列对原文有关内容的分析和概括,不正确的一项是( )(3分)
A.主父偃早年并不得志,在通过卫青向皇上推荐但“上不召”的情况下,上书汉武帝,才
得到汉武帝的赏识和任用。 |
B.主父偃向武帝进献了“推恩术”,表面上推恩皇族子孙,实际上是将诸侯国化整为零,
削弱封国实力,武帝采纳了这一建议。 |
C.主父偃揭发燕王犯罪的事情后,大臣们都畏惧主父偃的口,贿赂和赠送给他的钱,累计
有千金之多。 |
| D.主父偃当了大官后,就揭发了燕王和赵王犯罪的事情。这是他对自己未显达时所受侮辱的报复。 |
【小题5】断句和翻译。(10分)
(1)用“/”给下面的文段断句。(3分)
余 虽 骨 肉 无 尺 寸 地 封 则 仁 孝 之 道 不 宣 愿 陛 下 令 诸 侯 得 推 恩分 子 弟 以 地 侯 之 彼 人 人 喜 得 所 愿 上 以 德 施 实 分 其 国 不 削 而 稍弱 矣 于 是 上 从 其 计。
(2)翻译下面的句子。(7分)
①齐诸儒生相与排摈,不容于齐。(3分)
②始吾贫时,昆弟不我衣食,宾客不我内门。(4分)

 23、如图,已知∠B=∠1,CD是△ABC的角平分线,求证:∠5=2∠4.请在下面横线上填出推理的依据:
23、如图,已知∠B=∠1,CD是△ABC的角平分线,求证:∠5=2∠4.请在下面横线上填出推理的依据: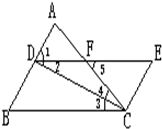 40、如图,已知∠B=∠1,CD是△ABC的角平分线.
40、如图,已知∠B=∠1,CD是△ABC的角平分线.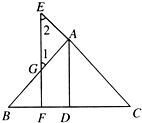 23、已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
23、已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.