
题目列表(包括答案和解析)

(牛顿定律的综合应用)物体A、B都静止在同一水平面上,它们的质量分别为mA、mB,与其水平面间的动摩擦因数分别为μA、μB.用平行于水平面的拉力F分别拉物体A、B,所得加速度a与拉力F关系图线分别如图中A、B所示,则可知
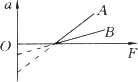
A.μA=μB,mB>mA
B.μA>μB,mB>mA
C.可能mB=mA
D.μA<μB,mB>mA
(2004·上海)(多普勒效应的综合应用)如图所示,声源S和观察者A都沿x轴正方向运动,相对于地面的速率分别为 和
和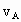 .空气中声音传播的速率为
.空气中声音传播的速率为 .设
.设 ,
, ,空气相对于地面没有流动.
,空气相对于地面没有流动.

(1)若声源相继发出两个声信号,时间间隔为 .请根据发出的这两个声信号从声源传播到观察者的过程,确定观察者接收到这两个信号的时间隔
.请根据发出的这两个声信号从声源传播到观察者的过程,确定观察者接收到这两个信号的时间隔 .
.
(2)请利用(1)的结果,推导此情形下观察者接收到的声波频率与声源发出的声波频率间的关系式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com