
题目列表(包括答案和解析)
在△ABC中,已知A(0,a),B(0,-a),(a为不等于零的常数)AC、BC两边所在的直线分别与x轴交于原点同侧的点M、N.设C(x0,y0).
(1)求M、N两点坐标(用(x0,y0)及α表示).
(2)若M、N满足![]() ,求点C的轨迹方程;
,求点C的轨迹方程;
(3)如果存在直线l∶y=kx-1(k≠0),使l与点C的轨迹相交于不同的P、Q两点,且![]() ,求α的取值范围.
,求α的取值范围.
如图,直线 与抛物线
与抛物线 (常数
(常数 )相交于不同的两点
)相交于不同的两点 、
、 ,且
,且 (
( 为定值),线段
为定值),线段 的中点为
的中点为 ,与直线
,与直线 平行的切线的切点为
平行的切线的切点为 (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(1)用 、
、 表示出
表示出 点、
点、 点的坐标,并证明
点的坐标,并证明 垂直于
垂直于 轴;
轴;
(2)求 的面积,证明
的面积,证明 的面积与
的面积与 、
、 无关,只与
无关,只与 有关;
有关;
(3)小张所在的兴趣小组完成上面两个小题后,小张连 、
、 ,再作与
,再作与 、
、 平行的切线,切点分别为
平行的切线,切点分别为 、
、 ,小张马上写出了
,小张马上写出了 、
、 的面积,由此小张求出了直线
的面积,由此小张求出了直线 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
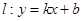 与抛物线
与抛物线 (常数
(常数 )相交于不同的两点
)相交于不同的两点 、
、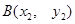 ,且
,且 (
(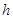 为定值),线段
为定值),线段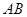 的中点为
的中点为 ,与直线
,与直线 平行的切线的切点为
平行的切线的切点为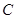 (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).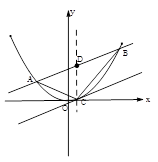
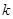 、
、 表示出
表示出 点、
点、 点的坐标,并证明
点的坐标,并证明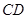 垂直于
垂直于 轴;
轴;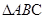 的面积,证明
的面积,证明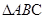 的面积与
的面积与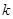 、
、 无关,只与
无关,只与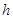 有关;
有关; 、
、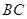 ,再作与
,再作与 、
、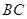 平行的切线,切点分别为
平行的切线,切点分别为 、
、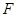 ,小张马上写出了
,小张马上写出了 、
、 的面积,由此小张求出了直线
的面积,由此小张求出了直线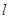 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com