
题目列表(包括答案和解析)
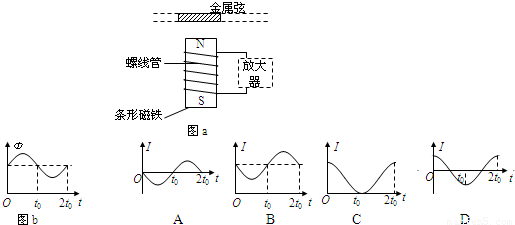
 (1)为观察电磁感应现象,某学生将电流表、螺线管A和B、蓄电池、开关用导线连接成如图所示的实验电路.当接通和断开开关时,电流表的指针将
(1)为观察电磁感应现象,某学生将电流表、螺线管A和B、蓄电池、开关用导线连接成如图所示的实验电路.当接通和断开开关时,电流表的指针将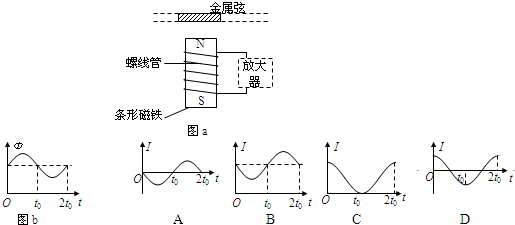

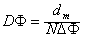 ,式中△φ为单匝试测线圈磁通量的变化量,则试测线圈所在处磁感应强度B=____。若将开关S从位置1拨到位置2的过程所用的时间为△t,则试测线圈P中产生的平均感应电动势
,式中△φ为单匝试测线圈磁通量的变化量,则试测线圈所在处磁感应强度B=____。若将开关S从位置1拨到位置2的过程所用的时间为△t,则试测线圈P中产生的平均感应电动势 =____。
=____。
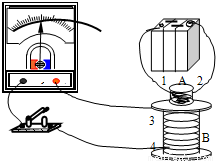
 如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置.将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀.将试测线圈引线的两端与冲击电流计D相连.拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转.
如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置.将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀.将试测线圈引线的两端与冲击电流计D相连.拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转.| dm |
| N△? |
| 实验次数 | I(A) | B(×10-3T) |
| 1 | 0.5 | 0.62 |
| 2 | 1.0 | 1.25 |
| 3 | 1.5 | 1.88 |
| 4 | 2.0 | 2.51 |
| 5 | 2.5 | 3.12 |
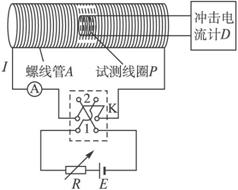
(1)将开关合到位置1,待螺线管A中的电流稳定后,再将K从位置1拨到位置2,测得D的最大偏转距离为Dm,已知冲击电流计的磁通灵敏度为Dφ,Dφ=![]() ,式中ΔΦ为单匝试测线圈磁通量的变化量.则试测线圈所在处磁感应强度B=__________;若将K从位置1拨到位置2的过程所用的时间为Δt,则试测线圈P中产生的平均感应电动势E=__________.
,式中ΔΦ为单匝试测线圈磁通量的变化量.则试测线圈所在处磁感应强度B=__________;若将K从位置1拨到位置2的过程所用的时间为Δt,则试测线圈P中产生的平均感应电动势E=__________.
(2)调节可变电阻R,多次改变电流并拨动K,得到A中电流I和磁感应强度B的数据,见下表.由此可得,螺线管A内部磁感应强度B和电流I的关系为B=__________.
实验次数 | I/A | B./×10-3 T |
1 | 0.5 | 0.62 |
2 | 1.0 | 1.25 |
3 | 1.5 | 1.88 |
4 | 2.0 | 2.51 |
5 | 2.5 | 3.12 |
(3)(多选题)为了减小实验误差,提高测量的准确性,可采取的措施有( )
A.适当增加试测线圈的匝数N B.适当增大试测线圈的横截面积S
C.适当增大可变电阻R的阻值 D.适当延长拨动开关的时间Δt
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com