
题目列表(包括答案和解析)
(1)如图3-3-4,转盘上有8个面积相等的扇形,转动转盘,求转盘停止转动时指针落在阴影部分的概率.
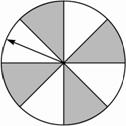
图3-3-4
(2)在500 mL的水中有一个草履虫,现从中随机取出2 mL水样放到显微镜下观察,求发现草履虫的概率.
P(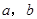 )是平面上的一个点,设事件A表示“
)是平面上的一个点,设事件A表示“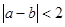 ”,其中
”,其中 为实常数.
为实常数.
(1)若 均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
(2)若 均为从区间[0,5)任取的一个数,求事件A发生的概率.
均为从区间[0,5)任取的一个数,求事件A发生的概率.
【解析】本试题考查了几何概型和古典概型结合的一道综合概率计算试题。首先明确区域中的所有基本事件数或者区域表示的面积,然后分别结合概率公式求解得到。
| 1 |
| x |
| 1 |
| a |
(1)抛掷两颗骰子,求出现两个“4点”的概率;

(2)如右图所示,图中有一转盘,甲、乙两人玩转盘游戏,规定当指针指向B区域时,甲获胜,否则乙获胜,求甲获胜的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com