
题目列表(包括答案和解析)
设a、b为正数,求证:不等式![]() +1>
+1>![]() ①成立的充要条件是:对于任意实数x>1,有ax+
①成立的充要条件是:对于任意实数x>1,有ax+![]() >b ②.
>b ②.
如下图所示,虚线部分是四个象限的角平分线,实线部分是函数y=f(x)的图象,则f(x)只可能是
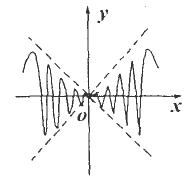
[ ]
已知三次函数f(x)=x(x-a)(x-b) 0<a<b
(1)当f(x)取得极值时x=s和x=t(s<t),求证:o<s<a<t<b;
(2)求f(x)的单调区间.
| |||||||||||
要采用分层抽样方法从100道选择题,50道判断题,20道解答题中选取22道题组成一份试卷,则从中选出填空题的道数是
[ ]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com