
题目列表(包括答案和解析)
 如图所示,在xoy平面直角坐标系第一象限内分布有垂直向外的匀强磁场,磁感应强度大小B=2.5×10-2T,在第二象限紧贴y轴和x轴放置一对平行金属板MN(中心轴线过y轴),极板间距d=0.4m,极板与左侧电路相连接.通过移动滑动头P可以改变极板MN间的电压.a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压U=
如图所示,在xoy平面直角坐标系第一象限内分布有垂直向外的匀强磁场,磁感应强度大小B=2.5×10-2T,在第二象限紧贴y轴和x轴放置一对平行金属板MN(中心轴线过y轴),极板间距d=0.4m,极板与左侧电路相连接.通过移动滑动头P可以改变极板MN间的电压.a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压U=
| ||
| 3 |
| q |
| m |
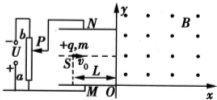
 如图所示,在xOy坐标的第一象限内分布有垂直xOy平面向外的匀强磁场,磁感应强度大小为B=2.5×10-2T.在第二象限紧贴y轴和x轴放置一对平行金属板MN(中心轴线垂直y轴),极板间距d=0.4m,极板与左侧电路相连接,通过移动滑动头P可以改变极板MN间的电压.a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压U=
如图所示,在xOy坐标的第一象限内分布有垂直xOy平面向外的匀强磁场,磁感应强度大小为B=2.5×10-2T.在第二象限紧贴y轴和x轴放置一对平行金属板MN(中心轴线垂直y轴),极板间距d=0.4m,极板与左侧电路相连接,通过移动滑动头P可以改变极板MN间的电压.a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压U=
| ||
| 3 |
| q |
| m |
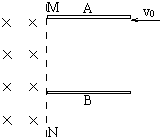 如图所示,A、B两平行板水平放置,板长L=0.2m,板间有方向竖直向下的匀强电场,场强E=2×103V/m,两板间距d=
如图所示,A、B两平行板水平放置,板长L=0.2m,板间有方向竖直向下的匀强电场,场强E=2×103V/m,两板间距d=
| ||
| 10 |
| q |
| m |
| 3 |
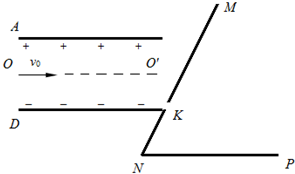 过小孔K:
过小孔K: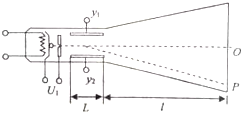 如图所示,为一示波管的示意图,阴极和阳极间的加速电压U1=2500V,偏转板y1和y2间的偏转电压为U2=200V,两板间距离为d=2.0cm,板长为L=6.0cm,偏转板右侧到荧光屏的距离为l=18.0cm.已知电子的质量m=0.90×10-30kg和电子的电荷量e=1.60×10-19C.从阴极发射出的电子(设初速为零),经阴极和阳极间电场加速后,又经匀强电场作用打在荧光屏的P点上,求:
如图所示,为一示波管的示意图,阴极和阳极间的加速电压U1=2500V,偏转板y1和y2间的偏转电压为U2=200V,两板间距离为d=2.0cm,板长为L=6.0cm,偏转板右侧到荧光屏的距离为l=18.0cm.已知电子的质量m=0.90×10-30kg和电子的电荷量e=1.60×10-19C.从阴极发射出的电子(设初速为零),经阴极和阳极间电场加速后,又经匀强电场作用打在荧光屏的P点上,求:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com