
题目列表(包括答案和解析)
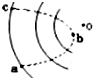 一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中虚线abc所示,图中实线是同心圆弧,表示电场的等势面.不计重力,可以判断( )
一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中虚线abc所示,图中实线是同心圆弧,表示电场的等势面.不计重力,可以判断( ) 一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( )
一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( ) 一带电粒子从电场中的A点运动到B点,运动轨迹如图中虚线所示,不计粒子所受重力,下列说法正确的是( )
一带电粒子从电场中的A点运动到B点,运动轨迹如图中虚线所示,不计粒子所受重力,下列说法正确的是( ) 一带电粒子射入一固定在O点的点电荷的电场中,粒子运动的轨迹如图所示,图中实线是同心圆弧,表示电场的等势面,不计重力,可以判断( )
一带电粒子射入一固定在O点的点电荷的电场中,粒子运动的轨迹如图所示,图中实线是同心圆弧,表示电场的等势面,不计重力,可以判断( )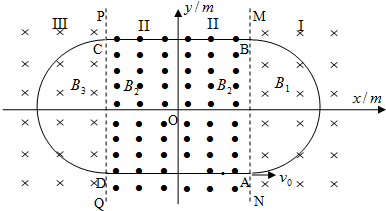
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com