练习册

  • 练习册
  • 试题
    (一)方法总结 1.极限的概念和运算法则是微积分中最重要的工具.也是学好导数的基础.它是历年高考的重点考查内容.多与分类讨论相结合.通常与数列结合的题目要多一些.解答时要求先求出数列的通项公式或是前项和公式再求极限.求函数的极限时.经常要用到常见函数的极限及两个重要极限(解决函数极限的小题时可用洛毕达法则).通过恒等变形用函数极限的四则运算法则求相关函数的极限.或利用初等函数在其定义域内每一点处的极限值等于该点函数值求函数的极限或利用函数的极限判定函数在给定点处的连续性.归纳法也是本章常见的考查点.一定要注意用数学归纳法解题时的步骤. 2.导数是中学限选内容中较为重要的知识.由于其应用的广泛性.为我们解决所学过的有关函数问题提供了一般性方法.是解决实际问题强有力的工具.导数的概念及其运算是导数应用的基础.是高考重点考查的对象.要牢记导数公式.熟练应用导数公式求函数的导数.掌握求导数的方法.应用导数解决实际问题的关键是要建立恰当的数学模型.了解导数概念的实际背景. 3.复数的概念.搞清楚实部与虚部.＝-1.共轭复数等概念.及复数和运算. 【查看更多】

     

    题目列表(包括答案和解析)

    16、用红、黄、蓝、白、黑五种颜色在“田”字形的4个小方格内，每格涂一种颜色，相邻（有公共边）两格涂不同的颜色，如果颜色可以反复使用，共有
    260
    种不同的涂色方法．
    1 2
    3 4

    查看答案和解析>>

    函数y=kx+b，其中k，b（k≠0）是常数，其图象是一条直线，称这个函数为线性函数，对于非线性可导函数f（x），在点x0附近一点x的函数值f（x），可以用如下方法求其近似代替值：f（x）≈f（x0）+f'（x0）（x-x0），利用这一方法，m=
    		3.996
    的近似代替值是
    1.999
    1.999
    ．

    查看答案和解析>>

    （2012•奉贤区二模）预测人口的变化趋势有多种方法，“直接推算法”使用的公式是Pn=P0（1+k）n（k＞-1），其中Pn为预测期人口数，P0为初期人口数，k为预测期内年增长率，n为预测期间隔年数．如果在某一时期有-1＜k＜0，那么在这期间人口数（　　）

    查看答案和解析>>

    预测人口的变化趋势有多种方法，“直接推算法”使用的公式是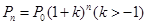，其中Pn为预测人口数，P0为初期人口数，k为预测年内增长率，n为预测期间隔年数．如果在某一时期有-1<k<0，那么这期间人口数 （    ）

        A．呈上升趋势   B．呈下降趋势

        C．摆动变化 D．不变

     

     

    查看答案和解析>>

    把10个苹果分成三堆,要求每一堆至少1个,至多5个,则不同的分类方法共有（    ）

    A.4种               B.5种                C.6种                 D.7种

    查看答案和解析>>


    同步练习册答案