
题目列表(包括答案和解析)
给出下列四个命题:
①若a>b>0,则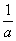 >
>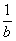 ; ②若a>b>0,则a-
; ②若a>b>0,则a- >b-
>b-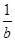 ; ③若a>b>0,则
; ③若a>b>0,则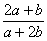 >
> ;
;
④若a>0,b>0,且a+b=1,则 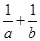 的最小值为4.
的最小值为4.
其中正确命题的序号是____ _.(把你认为正确命题的序号都填上)[来源:Zxxk.Com]
若a>0, b>0, 且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( )
A. 2 B. 3 C. 6 D. 9
若a>0,b>0,a+b=2,则下列不等式对一切满足条件的a、b恒成立的是 (写出所有正确命题的编号).
①ab≤1;② +
+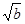 ≤
≤ ;③a2+b2≥2;④a3+b3≥3;⑤
;③a2+b2≥2;④a3+b3≥3;⑤ +
+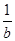 ≥2.
≥2.
下列命题正确的序号为 .
①函数y=ln(3-x)的定义域为(-∞,3];
②定义在[a,b]上的偶函数f(x)=x2+(a+5)x+b的最小值为5;
③若命题p:对∀x∈R,都有x2-x+2≥0,则命题![]() p:∃x0∈R,有
p:∃x0∈R,有![]() -x0+2<0;
-x0+2<0;
④若a>0,b>0,a+b=4,则![]() +
+![]() 的最小值为1.
的最小值为1.
若a>0,b>0,且a+b=2,则下列不等式恒成立的是( )
(A)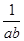 >1
(B)
>1
(B) +
+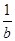 ≤2
≤2
(C) ≥1 (D)a2+b2≥2
≥1 (D)a2+b2≥2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com