
题目列表(包括答案和解析)
|
起始月薪(百元) |
[13,14) |
[14,15) |
[15,16) |
[16,17) |
[17,18) |
[18,19) |
[19,20) |
[20,21) |
|
频数 |
7 |
11 |
26 |
23 |
15 |
8 |
4 |
6 |
(1)列出样本的频率分布表(含累积频率);
(2)画出频率分布直方图和累积频率分布图;
(3)根据累积频率分布估计该校毕业生起始月薪低于2000元的概率;
(4)估计起始月薪的数学期望。
有一个容量为100的某校毕业生起始月薪的样本,数据的分组及各组的频数如下:
|
起始月薪(百元) |
[13,14) |
[14,15) |
[15,16) |
[16,17) |
[17,18) |
[18,19) |
[19,20) |
[20,21) |
|
频数 |
7 |
11 |
26 |
23 |
15 |
8 |
4 |
6 |
(1)列出样本的频率分布表(含累积频率);
(2)画出频率分布直方图和累积频率分布图;
(3)根据累积频率分布估计该校毕业生起始月薪低于2000元的概率;
(4)估计起始月薪的数学期望。
A、
| ||
B、
| ||
C、
| ||
D、
|
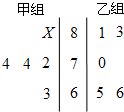 如图所示茎叶图记录了甲乙两组各5名同学的数学成绩.甲组成绩中有一个数据模糊,无法确认,在图中以X表示.若两个小组的平均成绩相同,则下列结论正确的是( )
如图所示茎叶图记录了甲乙两组各5名同学的数学成绩.甲组成绩中有一个数据模糊,无法确认,在图中以X表示.若两个小组的平均成绩相同,则下列结论正确的是( )| A、X=2,S甲2<S乙2 | B、X=2,S甲2>S乙2 | C、X=6,S甲2<S乙2 | D、X=6,2,S甲2>S乙2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com