
题目列表(包括答案和解析)
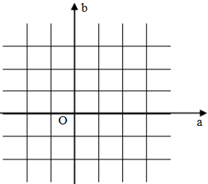 已知关于x的二次函数f(x)=x2+ax-b(a,b∈R).
已知关于x的二次函数f(x)=x2+ax-b(a,b∈R).| OP |
| OA1 |
| OA2 |
| OP |
| OA1 |
| OA2 |
| OAn |
(1)当n=3时,求捕鱼收益的期望值;
(2)试求n的值,使这次远洋捕鱼收益的期望值达到最大.
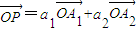 ,求证:a1+a2=1;
,求证:a1+a2=1;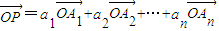 成立?请说明你的理由.
成立?请说明你的理由.必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
第Ⅰ卷 选择题(共50分)
一、选择题(本大题共10小题,每小题5分,满分50分)
 1、设全集U={
1、设全集U={![]() 是不大于9的正整数},
是不大于9的正整数},![]() {1,2,3 },
{1,2,3 },![]() {3,4,5,6}则图中阴影部分所表示的集合为( )
{3,4,5,6}则图中阴影部分所表示的集合为( )
A.{1,2,3,4,5,6} B. {7,8,9}
C.{7,8} D. {1,2,4,5,6,7,8,9}
2、计算复数(1-i)2-![]() 等于( )
等于( )
A.0 B.2 C. 4i D. -4i
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com