
题目列表(包括答案和解析)
消费金额(元)的范围 | [200,400) | [400,500) | [500,700) | [700,900) | … |
获得奖券的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在该商场购物可以获得双重优惠.例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为400×0.2+30=110(元).设购买商品得到的优惠率=![]() .试问:
.试问:
(1)若购买一件标价为1 000元的商品,顾客得到的优惠率是多少?
(2)对于标价在[500,800](元)内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?
的优惠率?
消费金额 (元)的范围 | [200,400) | [400,500) | [500,700) | [700,900] | … |
获得奖券 的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为:400×0.2+30=110元.
设购买商品得到的优惠率=![]() ,试问:
,试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在[500,800](元)内的商品,顾客购买标价为多少元的商品,可得到不少于![]() 的优惠率?
的优惠率?
某商场在促销期间规定:商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券:
|
消费金额(元)的范围 |
[200,400] |
[400,500) |
[500,700] |
[700,900] |
… |
|
获得奖券的金额(元) |
30 |
60 |
100 |
130 |
… |
根据上述促销方法,顾客在该商场购物可以获得双重优惠.例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为:400×0.2+30=110(元).设购买商品得到的优惠率=![]() .试问:
.试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在[500,800](元)内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?
的优惠率?
|
消费金额(元)的范围 |
[200,400] |
[400,500) |
[500,700] |
[700,900] |
… |
|
获得奖券的金额(元) |
30 |
60 |
100 |
130 |
… |
根据上述促销方法,顾客在该商场购物可以获得双重优惠.例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为:400×0.2+30=110(元).设购买商品得到的优惠率=![]() .试问:
.试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在[500,800](元)内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?
的优惠率?
提高大桥的车辆通行能力可改善整个城市的交通状况.一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当车流密度不超过50辆/千米时,车流速度为30千米/小时.研究表明:当50<x≤200时,车流速度v与车流密度x满足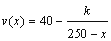 ,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
(Ⅰ) 当0<x≤200时,求函数v(x)的表达式;
(Ⅱ) 当车流密度x为多大时,车流量(单位时间内通过桥上观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到个位,参考数据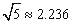 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com