
题目列表(包括答案和解析)
(本题满分14分,第(1)小题6分,第(2)小题8分)
(1)已知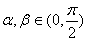 ,且
,且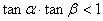 ,比较
,比较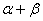 与
与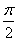 的大小;
的大小;
(2)试确定一个区间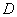 ,
,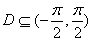 ,对任意的
,对任意的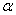 、
、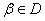 ,当
,当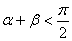 时,恒有
时,恒有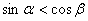 ;并说明理由。
;并说明理由。
说明:对于第(2)题,将根据写出区间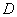 所体现的思维层次和对问题探究的完整性,给予不同的评分.
所体现的思维层次和对问题探究的完整性,给予不同的评分.
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
对于定义域为![]() 的函数
的函数![]() ,若有常数M,使得对任意的
,若有常数M,使得对任意的![]() ,存在唯一的
,存在唯一的![]() 满足等式
满足等式![]() ,则称M为函数
,则称M为函数![]() f (x)的“均值”.
f (x)的“均值”.
(1)判断0是否为函数![]() ≤
≤![]() ≤
≤![]() 的“均值”,请说明理由;
的“均值”,请说明理由;
(2)若函数![]()
![]() 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围;
(3)已知函数![]() 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数![]() 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
说明:对于(3),将根据结论的完整性与一般性程度给予不同的评分.
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
对于定义域为![]() 的函数
的函数![]() ,若有常数M,使得对任意的
,若有常数M,使得对任意的![]() ,存在唯一的
,存在唯一的![]() 满足等式
满足等式![]() ,则称M为函数
,则称M为函数![]() f (x)的“均值”.
f (x)的“均值”.
(1)判断1是否为函数![]() ≤
≤![]() ≤
≤![]() 的“均值”,请说明理由;
的“均值”,请说明理由;
(2)若函数![]()
![]() 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围;
(3)若函数![]() 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数![]() 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
说明:对于(3),将根据结论的完整性与一般性程度给予不同的评分
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
对于定义域为![]() 的函数
的函数![]() ,若有常数M,使得对任意的
,若有常数M,使得对任意的![]() ,存在唯一的
,存在唯一的![]() 满足等式
满足等式![]() ,则称M为函数
,则称M为函数![]() f (x)的“均值”.
f (x)的“均值”.
(1)判断0是否为函数![]() ≤
≤![]() ≤
≤![]() 的“均值”,请说明理由;
的“均值”,请说明理由;
(2)若函数![]()
![]() 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围;
(3)已知函数![]() 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数![]() 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
说明:对于(3),将根据结论的完整性与一般性程度给予不同的评分.
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
对于定义域为![]() 的函数
的函数![]() ,若有常数M,使得对任意的
,若有常数M,使得对任意的![]() ,存在唯一的
,存在唯一的![]() 满足等式
满足等式![]() ,则称M为函数
,则称M为函数![]() f (x)的“均值”.
f (x)的“均值”.
(1)判断1是否为函数![]() ≤
≤![]() ≤
≤![]() 的“均值”,请说明理由;
的“均值”,请说明理由;
(2)若函数![]()
![]() 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围;
(3)若函数![]() 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数![]() 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
说明:对于(3),将根据结论的完整性与一般性程度给予不同的评分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com