（07年安徽卷）（本小题满分14分）

　　　某国采用养老储备金制度，公民在就业的第一年就交纳养老储备金，数目为a₁,以后第年交纳的数目均比上一年增加d(d>0),因此，历年所交纳的储备金数目a₁,a₂,…是一个公差为d的等差数列，与此同时，国家给予优惠的计息政策，不仅采用固定利率，而且计算复利，这就是说，如果固定年利率为r(r>0)，那么，在第n年末，第一年所交纳的储备金就变为n(1+r)^n-1，第二年所交纳的储备金就变为a₂(1+r)^n-2,……，以T_n表示到第n年末所累计的储备金总额.

　（Ⅰ）写出T_n与T_n-1（n≥2）的递推关系式；

　（Ⅱ）求证：T_n=A_n+B_n，其中是一个等比数列，是一个等差数列.

（本小题满分14分）

　　已知：函数是定义在上的偶函数，当时，为实数）.

　　（1）当时，求的解析式；

　　（2）若，试判断上的单调性，并证明你的结论；

　　（3）是否存在，使得当有最大值1？若存在，求出的值;若不存在，请说明理由.

（本小题满分14分）　（参考公式：）

设函数，

（1）令，判断并证明在（-1，+∞）上的单调性，求；

（2）求在定义域上的最小值；

（3）是否存在实数、满足，使得在区间上的值域也为？

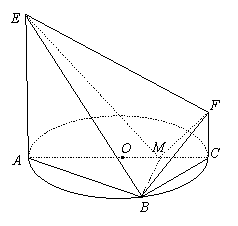
（本小题满分14分）

　 如图，是圆的直径，点在圆上，，交于点，平面，，．

（1）证明：；

（2）求平面与平面所成的锐二面角的余弦值．

（本小题满分14分）　（参考公式：）

设函数，

（1）令，判断并证明在（-1，+∞）上的单调性，求；

（2）求在定义域上的最小值；

（3）是否存在实数、满足，使得在区间上的值域也为？