练习册

  • 练习册
  • 试题
    分析法与综合法是对立统一的两个方面.前者执果索因.利于思考.因为它方向明确.思路自然.易于掌握,后者是由因导果.宜于表述.因为它条理清晰.形式简洁.适合人们的思维习惯.但是.用分析法探求证明不等式.只是一种重要的探求方式.而不是一种好的书写形式.因为它叙述较繁.如果把“只需证明 等字眼不写.就成了错误.而用综合法书写的形式.它掩盖了分析.探索的过程.因而证明不等式时.分析法.综合法常常是不能分离的.如果使用综合法证明不等式.难以入手时常用分析法探索证题的途径.之后用综合法形式写出它的证明过程.以适应人们习惯的思维规律.还有的不等式证明难度较大.需一边分析.一边综合.实现两头往中间靠以达到证题的目的.这充分表明分析与综合之间互为前提.互相渗透.互相转化的辩证统一关系.分析的终点是综合的起点.综合的终点又成为进一步分析的起点. 【查看更多】

     

    题目列表(包括答案和解析)

    若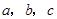是不全相等的实数，求证：．

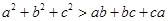    证明过程如下：

    ，，，，

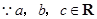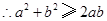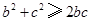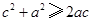    又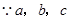不全相等，

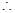    以上三式至少有一个“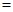”不成立，

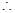    将以上三式相加得，

    ．

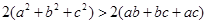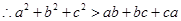    此证法是（    ）

    A．分析法       B．综合法       C．分析法与综合法并用       D．反证法

     

    查看答案和解析>>

    若a，b，c是不全相等的实数，求证：a2＋b2＋c2>ab＋bc＋ca.

    证明过程如下：

    ∵a、b、c∈R，∴a2＋b2≥2ab，

    b2＋c2≥2bc，c2＋a2≥2ac，

    又∵a，b，c不全相等，

    ∴以上三式至少有一个“＝”不成立，

    ∴将以上三式相加得2(a2＋b2＋c2)>2(ab＋bc＋ac)，

    ∴a2＋b2＋c2>ab＋bc＋ca.

    此证法是(　　)

    (A)分析法                      (B)综合法

    (C)分析法与综合法并用      (D)反证法

    查看答案和解析>>

    求证：－1＞－．证明：要证－1＞－，只需证＋＞＋1，即证7＋2＋5＞11＋2＋1，＞，因为35＞11，所以原不等式成立．以上证明运用了

    [　　]
    A．

    分析法

    B．

    综合法

    C．

    分析法与综合法综合使用

    D．

    间接证明

    查看答案和解析>>

    以下方法不能用于证明不等式的是


    1. A.
      比较法
    2. B.
      随机抽样法
    3. C.
      综合法与分析法
    4. D.
      反证法与放缩法

    查看答案和解析>>

    分析与综合法证明不等式：已知a+b+c=0，求证：ab+bc+ca≤0．

    查看答案和解析>>


    同步练习册答案