
题目列表(包括答案和解析)
在一堂物理课上,老师要求学生只用50 g和5 g两个砝码以及天平将现有495 g食盐平均分成三份,现在请你为他们设计一个算法,使称量的次数最少.试问需称量多少次.
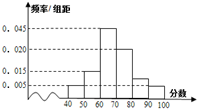 某校对参加数学竞赛的学生中随机选取40名学生的成绩作为样本,这40名学生的成绩全部在40分到100之间,现将成绩按如下方式分成6组,即:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]据此绘制如图所示的频率直方图,在选取的40名学生中
某校对参加数学竞赛的学生中随机选取40名学生的成绩作为样本,这40名学生的成绩全部在40分到100之间,现将成绩按如下方式分成6组,即:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]据此绘制如图所示的频率直方图,在选取的40名学生中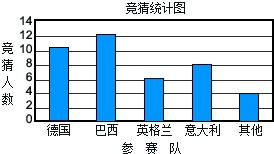
(8分)对某校高一年级学生参加社区服务次数进行统计,随机抽取 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
|
分组 |
频数 |
频率 |
|
|
10 |
0.25 |
|
|
25 |
|
|
|
|
|
|
|
2 |
0.05 |
|
合计 |
M |
1 |
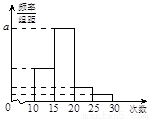
⑴求出表中 、
、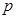 及图中
及图中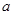 的值;
的值;
⑵若该校高一学生有720人,试估计他们参加社区服务的次数在区间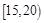 内的人数;
内的人数;
⑶在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间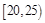 内的概率.
内的概率.
(本小题满分13分)
对某校高三年级学生参加社区服务次数进行统计,随机抽取 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(Ⅰ)求出表中 及图中
及图中 的值;
的值;
(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间 内的人数;
内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间 内的概率.
内的概率.

|
分组 |
频数 |
频率 |
|
|
10 |
0.25 |
|
|
24 |
|
|
|
|
|
|
|
2 |
0.05 |
|
合计 |
|
1 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com