
题目列表(包括答案和解析)
下列语句表达不是算法的是
利用平面内两点间的距离公式求平面内M(0,0)与N(2,2)两点间的距离
从长沙到北京的火车票是300元
利用公式法解方程2x2+x-1=0
利用公式S=πr2,计算半径为3的圆的面积
| x2 |
| |an| |
| y2 |
| 4 |
在等差数列![]() 中,
中,![]() ,
,![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项之和,曲线
项之和,曲线![]() 的方程是
的方程是![]() ,直线
,直线![]() 的方程是
的方程是![]() .
.
求数列![]() 的通项公式;
的通项公式;
当直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() 时,令
时,令![]() ,
,
求![]() 的最小值;
的最小值;
对于直线![]() 和直线外的一点P,用“
和直线外的一点P,用“![]() 上的点与点P距离的最小值”定义点P到直线
上的点与点P距离的最小值”定义点P到直线![]() 的距离与原有的点到直线距离的概念是等价的,若曲线
的距离与原有的点到直线距离的概念是等价的,若曲线![]() 与直线
与直线![]() 不相交,试以类似的方式给出一条曲线
不相交,试以类似的方式给出一条曲线![]() 与直线
与直线![]() 间“距离”的定义,并依照给出的定义,在
间“距离”的定义,并依照给出的定义,在![]() 中自行选定一个椭圆,求出该椭圆与直线
中自行选定一个椭圆,求出该椭圆与直线![]() 的“距离”.
的“距离”.
 +
+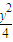 =1,直线l的方程是y=x+3.
=1,直线l的方程是y=x+3.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com