
题目列表(包括答案和解析)
(1)求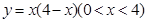 的最大值,并求
的最大值,并求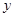 取最大值时相应的
取最大值时相应的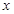 的值.
的值.
(2)若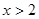 ,求
,求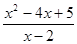 的最小值.
的最小值.
【解析】本试题主要是考查了不等式的最值思想,以及运用均值不等式求解最值的问题。
若函数![]()
![]() 能用均值不等式求最大值,则需要补充
能用均值不等式求最大值,则需要补充![]() 的取值范围是_________.
的取值范围是_________.
| x2+4 |
| 1 |
| 2 |
| x2+4 |
| x2+4 |
| g(x) |
如图所示,某公园要在一块绿地的中央修建两个相同的矩形的池塘,每个面积为10000米2,池塘前方要留4米宽的走道,其余各方为2米宽的走道,问每个池塘的长宽各为多少米时占地总面积最少?

【解析】本试题主要考查了函数在实际中的运用。运用均值不等式求解函数的最值的运用。
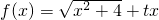 (x∈R)
(x∈R)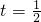 时,可以将f(x)化成
时,可以将f(x)化成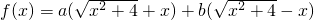 的形式,运用基本不等式求f(x)的最小值及此时x的取值;
的形式,运用基本不等式求f(x)的最小值及此时x的取值;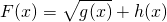 ,利用基本不等式研究函数F(x)的最值问题.
,利用基本不等式研究函数F(x)的最值问题.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com