
题目列表(包括答案和解析)
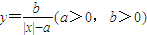 的函数因其图象类似于汉字“囧”字,故生动地称为“囧函数”,并把其与y轴的交点关于原点的对称点称为“囧点”,以“囧点”为圆心凡是与“囧函数”有公共点的圆,皆称之为“囧圆”,则当a=1,b=1时,所有的“囧圆”中,面积的最小值为( )
的函数因其图象类似于汉字“囧”字,故生动地称为“囧函数”,并把其与y轴的交点关于原点的对称点称为“囧点”,以“囧点”为圆心凡是与“囧函数”有公共点的圆,皆称之为“囧圆”,则当a=1,b=1时,所有的“囧圆”中,面积的最小值为( )我们把形如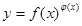 的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边取对数得 ,两边对x求导数,得
,两边对x求导数,得 于是
于是 ,运用此方法可以求得函数
,运用此方法可以求得函数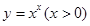 在(1,1)处的切线方程是 .
在(1,1)处的切线方程是 .
我们把形如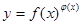 的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数:在函数解析式两边求对数得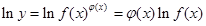 ,两边对
,两边对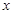 求导数,得
求导数,得 于是
于是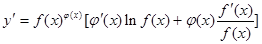 ,运用此方法可以求得函数
,运用此方法可以求得函数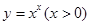 在(1,1)处的切线方程是 _________
在(1,1)处的切线方程是 _________
 的函数因其图象类似于汉字“囧”字,故生动地称为“囧函数”,并把其与y轴的交点关于原点的对称点称为“囧点”,以“囧点”为圆心凡是与“囧函数”有公共点的圆,皆称之为“囧圆”,则当a=1,b=1时,所有的“囧圆”中,面积的最小值为 .
的函数因其图象类似于汉字“囧”字,故生动地称为“囧函数”,并把其与y轴的交点关于原点的对称点称为“囧点”,以“囧点”为圆心凡是与“囧函数”有公共点的圆,皆称之为“囧圆”,则当a=1,b=1时,所有的“囧圆”中,面积的最小值为 .我们把形如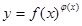 的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得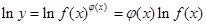 ,两边对x求导数,得
,两边对x求导数,得 于是
于是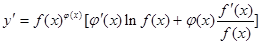 ,运用此方法可以求得函数
,运用此方法可以求得函数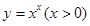 在(1,1)处的切线方程是 ▲
.
在(1,1)处的切线方程是 ▲
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com