练习册

  • 练习册
  • 试题
    ∴ 解:(2) 要使极限存在1-a2=0. ∴ 即1+2ab=0.a+1≠0. ∴ 解:(3) 当x→1时极限存在.则分子.分母必有公因式x-1. ∴a-b2=-1 ∴原式= ∴ 说明:第一题是分子分母同除以x的较低的幂.第二题是分子有理化.和第一题的方法相结合.第三题是因式分解法和分子有理化法相结合. 我们以前求极限的一种方法是分子.分母同除x的最高次幂.但像第一题.因为分子的次数低于分母的次数.如果分子除以x2.则分子极限为0.不符合.所以通分后.应除以分子分母中x的较低次幂.并且x的次数比分子x的最高次幂大的项的系数应该等于0.这样极限才存在. 例3 f(x)=求a.使f(x)存在. 解:要使f(x)存在.则f(x)与f(x)要存在且相等. f(x)= (2x2-3)=2·22-3=5. f(x)= (3x2+a)=3·22+a=12+a. ∴5=12+a.∴a=-7 例4设函数f(x)=.在x=0处连续.求a.b的值. 分析:要使f(x)在x=0处连续.就要使f(x)在x=0处的左.右极限存在.并且相等.等于f(x)在x=0处的值a. 解:f(x)=·(-1) f(x)=(2x+1)=2·0+1=1 ∴ 说明:这类连续的题目.也关键是求在一点处的左.右极限存在并都等于在这点的函数值.与函数在这点的极限存在的方法是相同的 【查看更多】

     

    题目列表(包括答案和解析)

    有一天哈利·波特在魔法学校里进行一种毒药实验,从盛满1升纯药液的容器中倒出升,然后用水填满,再倒出升,又用水填满.

    (1)这样进行5次,则容器中剩下的纯药液的升数为多少？

    (2)如果哈利·波特决定要用原药液毒性的10%,问重复这样的过程,几次可以达到？

    (3)如果哈利·波特决定用函数图象来解第(2)问,你能帮他一下吗？

    查看答案和解析>>

    某市在2000年的人口总数约为1000万人．

    (1)如果该市人口自然增长率控制在1.15％，大约经过多少年以后，该市人口总数将达到1200万人(精确到年)；

    (2)要使该市人口总数在2020年时不超过1200万人，人口的年自然增长率应控制在多少？(精确到0.1％)．

    以下数据供选用：lg1.2＝0.07918，lg1.0115＝0.004965，100.003959＝1.0091．

    查看答案和解析>>

    有一天哈利·波特在魔法学校里进行一种毒药实验，从盛满1升纯药液的容器中倒出升，然后用水填满，再倒出升，又用水填满．

    (1)这样进行5次，则容器中剩下的纯药液的升数为多少？

    (2)如果哈利·波特决定要用原药液毒性的10%，问重复这样的过程，几次可以达到？

    (3)如果哈利·波特决定用函数图象来解第(2)问，你能帮他一下吗？

    查看答案和解析>>

    命题P“方程log
    1
    2
    (a-2x)=2+x    有解”是命题Q“方程x2-2x+a=0无实根”的（　　）条件．

    查看答案和解析>>

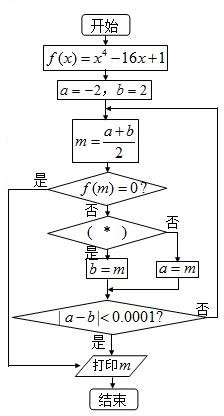    （2013•韶关三模）如图是用二分法求方程x4-16x+1=0在[-2，2]的近似解的程序框图，要求解的精确度为0.0001，则（*）处应填的内容是
    f（a）•f（m）＜0或f（b）•f（m）＞0
    f（a）•f（m）＜0或f（b）•f（m）＞0
    ．

    查看答案和解析>>


    同步练习册答案