2．学习二次函数.可以从两个方面入手:一是解析式.二是图像特征. 从解析式出发.可以进行纯粹的代数推理.这种代数推理.论证的能力反映出一个人的基本数学素养,从图像特征出发.可以实现数与形的自然结合.这——青夏教育精英家教网—

2．学习二次函数.可以从两个方面入手:一是解析式.二是图像特征. 从解析式出发.可以进行纯粹的代数推理.这种代数推理.论证的能力反映出一个人的基本数学素养,从图像特征出发.可以实现数与形的自然结合.这正是中学数学中一种非常重要的思想方法. 本文将从这两个方面研究涉及二次函数的一些综合问题. 由于二次函数的解析式简捷明了.易于变形(一般式.顶点式.零点式等).所以.在解决二次函数的问题时.常常借助其解析式.通过纯代数推理.进而导出二次函数的有关性质. (1)二次函数的一般式中有三个参数. 解题的关键在于:通过三个独立条件“确定这三个参数. (2)数形结合:二次函数的图像为抛物线.具有许多优美的性质.如对称性.单调性.凹凸性等.结合这些图像特征解决有关二次函数的问题.可以化难为易.形象直观.因为二次函数在区间和区间上分别单调.所以函数在闭区间上的最大值.最小值必在区间端点或顶点处取得,函数在闭区间上的最大值必在区间端点或顶点处取得. 【查看更多】

题目列表(包括答案和解析)

（本小题13分）已知关于x的一元二次函数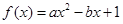，分别从集合P和Q中随机取一个数a和b得到数列。

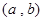（1）若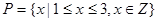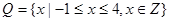，，列举出所有的数对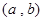，并求函数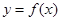有零点的概率；

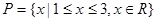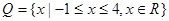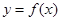（2）若，，求函数在区间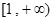上是增函数的概率。

查看答案和解析>>

（2003•崇文区一模）某化肥厂从今年1月起，若不改善生产环境，按现状生产，每月收入为70万元，同时还将受到环保部门的处罚，第1个月罚1万元，以后逐月递增2万元．如果从今年1月起投资400万元增加回收净化设备（改造设备时间不计），一方面可以改善环境，免去环保部门的处罚，另一方面也可降低原料成本，据测算，投产后的前5个月中的累计收入y（万元）是生产时间n（以月为单位）的二次函数．生产前1、前2、前3个月的累计收入分别可达101万元、204万元和309万元，以后每个月的收入稳定在第5个月的水平．
（I）求投资改造设备后，累计收入y与生产时间n的函数表达式；
（II）至少经过多少个月，投资改造设备后的纯收入多于不改造设备时的纯收入？

查看答案和解析>>

7、从-2、-1、0、1、2、3这六个数字中任选3个不重复的数字作为二次函数y=ax²+bx+c的系数a、b、c，则可以组成顶点在第一象限且过原点的抛物线条数为（　　）

A、6

B、20

C、100

D、120

查看答案和解析>>

下列函数关系中，可以看作二次函数y=ax²+bx+c模型的是（　　）

A．汽车的行驶公里数与耗油量的关系

B．我国人口年自然增长率为1%，这样我国人口总数随年份的变化关系

C．竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）

D．核电站中，作为核燃料的某放射元素裂变后所剩的原子数随使用时间的变化关系