练习册

  • 练习册
  • 试题
    近年来.立体几何高考命题形式比较稳定.题目难易适中.常常立足于棱柱.棱锥和正方体.复习是要以多面体为依托.始终把直线与直线.直线与平面.平面与平面垂直的性质和判定作为考察重点.在难度上也始终以中等偏难为主.在新课标教材中将立体几何要求进行了降低.重点在对图形及几何体的认识上.实现平面到空间的转化.示知识深化和拓展的重点.因而在这部分知识点上命题.将是重中之重. 预测2007年高考将以多面体为载体直接考察线面位置关系: (1)考题将会出现一个选择题.一个填空题和一个解答题, (2)在考题上的特点为:热点问题为平面的基本性质.考察线线.线面和面面关系的论证.此类题目将以客观题和解答题的第一步为主. (3)解答题多采用一题多问的方式.这样既降低了起点又分散了难点. 【查看更多】

     

    题目列表(包括答案和解析)

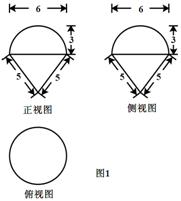
    （2012年高考（广东文））(立体几何)某几何体的三视图如图1所示,它的体积为    （　　）

    A．     B．     C．     D．

    查看答案和解析>>

    （2012年高考（北京文））近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):

    “厨余垃圾”箱

    “可回收物”箱

    “其他垃圾”箱

    厨余垃圾

    400

    100

    100

    可回收物

    30

    240

    30

    其他垃圾

    20

    20

    60

    (1)试估计厨余垃圾投放正确的概率;

    (2)试估计生活垃圾投放错误的概率;

    (3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为,其中,.当数据的方差最大时,写出的值(结论不要求证明),并求此时的值.

    (注:方差,其中为的平均数)

    查看答案和解析>>

    （2012年高考（广东理））(立体几何)某几何体的三视图如图1所示,它的体积为    （　　）

    A．     B．     C．     D．

    查看答案和解析>>

    记三角形面积为S，三条边长分别为a，b，c，内切圆半径为r，则平面几何有性质：S=
    1
    2
    （a+b+c）•r．若记四面体的体积为V，四个面面积分别为S1，S2，S3，S4，内切球半径为R，请你用类比方法写出立体几何中相似的性质
    V=
    1
    3
    （S1+S2+S3+S4）•R
    V=
    1
    3
    （S1+S2+S3+S4）•R
    ．

    查看答案和解析>>

    （2007•广州模拟）一高考考生咨询中心有A、B、C三条咨询热线．已知某一时刻热线A、B占线的概率均为0.5，热线C占线的概率为0.4，各热线是否占线相互之间没有影响，假设该时刻有ξ条热线占线，试求随机变量ξ的分布列和它的期望．

    查看答案和解析>>


    同步练习册答案