
题目列表(包括答案和解析)
定义在R上的函数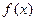 满足
满足 且函数
且函数 为奇函数,给
为奇函数,给
出下了命题:(1)函数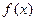 的最小正周期为
的最小正周期为 ,(2))函数
,(2))函数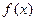 的图像关于点
的图像关于点 对称,(3)
对称,(3)
函数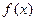 的图像关于
的图像关于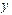 对称,则其中正确的命题序
对称,则其中正确的命题序 号是
号是
定义在R上的函数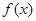 满足
满足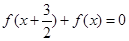 且函数
且函数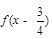 为奇函数,给
为奇函数,给
出下了命题:(1)函数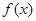 的最小正周期为
的最小正周期为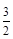 ,(2))函数
,(2))函数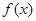 的图像关于点
的图像关于点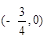 对称,(3)
对称,(3)
函数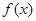 的图像关于
的图像关于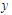 对称,则其中正确的命题序号是
对称,则其中正确的命题序号是
 满足
满足 且函数
且函数 为奇函数,给
为奇函数,给 的最小正周期为
的最小正周期为 ,(2))函数
,(2))函数 的图像关于点
的图像关于点 对称,(3)
对称,(3) 的图像关于
的图像关于 对称,则其中正确的命题序
对称,则其中正确的命题序 号是
号是
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| A.3 | B.2 | C.1 | D.0 |
Ⅰ选择题
1.C 2. B 3. B 4.B 5.A 6.C 7.A 8.C 9.D 10.A 11.C 12.C
Ⅱ非选择题
13.  14.
14. 
 15.
15. 16. (2) (3)
16. (2) (3)
17. 解:  (4分)
(4分)
(1)增区间为:  , 减区间为:
, 减区间为: (8分)
(8分)
(2) (12分)
(12分)
18.解:因骰子是均匀的,所以骰子各面朝下的可能性相等,设其中一枚骰子朝下的面上的数字为x,另一枚骰子朝下的面上的数字为y,则 的取值如下表:
的取值如下表:

x+y y
x
1
2
3
5
1
2
3
4
6
2
3
4
5
7
3
4
5
6
8
5
6
7
8
10
从表中可得: (8分)
(8分)
(2)p( =奇数)
=奇数)

 ………………12分
………………12分
19.解:(1)

∴ (2分)
(2分)
又  恒成立 ∴
恒成立 ∴
∴ ∴
∴
∴ (6分)
(6分)
(2)
∴
∴ ①)当  时, 解集为
时, 解集为
②当  时,解集为
时,解集为
③当  时,解集为
时,解集为 (12分)
(12分)
20.解:PD⊥面ABCD ∴DA、DC、DP 相互垂直
建立如图所示空间直角坐标系Oxyz
(1)


 ∴
∴



∴

 ∴PC⊥DA , PC⊥DE
∴PC⊥DA , PC⊥DE
∴PC⊥面ADE (4分)
(2)∵PD⊥面ABCD PC⊥平面ADE
∴PD与PC夹角为所求
 ∴ 所求二面角E-AD-B的大小为
∴ 所求二面角E-AD-B的大小为 (8分)
(8分)
(3)由(2)得:四边形ADFE为直角梯形,且 EF=1,DF= ,AD=2
,AD=2
∴ 
∴ 所求部分体积  (12分)
(12分)
21.解:(1)


 为等比数列
为等比数列 






 (4分)
(4分)
(2)



 (6分)
(6分)
(3)






 (7分)
(7分)






 (10分)
(10分)
∴M≥6 
















 (12分)
(12分)
22.解:(1)直线AB的方程为: 与抛物线的切点设为T
与抛物线的切点设为T 且
且
 ∴
∴


∴抛物线c的方程为:  (3分)
(3分)
⑵设直线l的方程为 :
: 易如:
易如:
设 ,
,


①M为AN中点 
由 (Ⅰ)、(Ⅱ)联解,得  代入(Ⅱ)
代入(Ⅱ)

 4
4
∴直线l的方程为 :  (7分)
(7分)
②
 (9分)
(9分)
FM为∠NFA的平分线
且
 (11分)
(11分)
又

 (14分)
(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com