
题目列表(包括答案和解析)
设函数 ,
, 的图象关于直线
的图象关于直线 对称,其中
对称,其中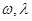 为常数,且
为常数,且 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)若 的图象经过点
的图象经过点 ,求函数
,求函数 在
在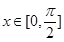 上的值域.
上的值域.
设函数 ,
, 的图象关于直线
的图象关于直线 对称,其中
对称,其中 为常数,且
为常数,且 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)若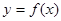 的图象经过点
的图象经过点 ,求函数
,求函数 在
在 上的值域.
上的值域.
 ,
, 的图象关于直线
的图象关于直线 对称,其中
对称,其中 为常数,且
为常数,且 .
. 的最小正周期;
的最小正周期; 的图象经过点
的图象经过点 ,求函数
,求函数 在
在 上的值域.
上的值域.设函数![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
(1) 求![]() 的值;
的值;
(2) 若直线![]() 与
与![]() 的图象无公共点,且
的图象无公共点,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
设函数![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
(1)求![]() 的值;
的值;
(2)判断并证明函数![]() 在区间(1,+∞)上的单调性;
在区间(1,+∞)上的单调性;
(3)若直线![]() =
=![]() (
(![]()
![]() R)与
R)与![]() 的图象无公共点,且
的图象无公共点,且![]() <
<![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
Ⅰ选择题
1.C 2. B 3. B 4.B 5.A 6.C 7.A 8.C 9.D 10.A 11.C 12.C
Ⅱ非选择题
13.  14.
14. 
 15.
15. 16. (2) (3)
16. (2) (3)
17. 解:  (4分)
(4分)
(1)增区间为:  , 减区间为:
, 减区间为: (8分)
(8分)
(2) (12分)
(12分)
18.解:因骰子是均匀的,所以骰子各面朝下的可能性相等,设其中一枚骰子朝下的面上的数字为x,另一枚骰子朝下的面上的数字为y,则 的取值如下表:
的取值如下表:

x+y y
x
1
2
3
5
1
2
3
4
6
2
3
4
5
7
3
4
5
6
8
5
6
7
8
10
从表中可得: (8分)
(8分)
(2)p( =奇数)
=奇数)

 ………………12分
………………12分
19.解:(1)

∴ (2分)
(2分)
又  恒成立 ∴
恒成立 ∴
∴ ∴
∴
∴ (6分)
(6分)
(2)
∴
∴ ①)当  时, 解集为
时, 解集为
②当  时,解集为
时,解集为
③当  时,解集为
时,解集为 (12分)
(12分)
20.解:PD⊥面ABCD ∴DA、DC、DP 相互垂直
建立如图所示空间直角坐标系Oxyz
(1)


 ∴
∴



∴

 ∴PC⊥DA , PC⊥DE
∴PC⊥DA , PC⊥DE
∴PC⊥面ADE (4分)
(2)∵PD⊥面ABCD PC⊥平面ADE
∴PD与PC夹角为所求
 ∴ 所求二面角E-AD-B的大小为
∴ 所求二面角E-AD-B的大小为 (8分)
(8分)
(3)由(2)得:四边形ADFE为直角梯形,且 EF=1,DF= ,AD=2
,AD=2
∴ 
∴ 所求部分体积  (12分)
(12分)
21.解:(1)


 为等比数列
为等比数列 






 (4分)
(4分)
(2)



 (6分)
(6分)
(3)






 (7分)
(7分)






 (10分)
(10分)
∴M≥6 
















 (12分)
(12分)
22.解:(1)直线AB的方程为: 与抛物线的切点设为T
与抛物线的切点设为T 且
且
 ∴
∴


∴抛物线c的方程为:  (3分)
(3分)
⑵设直线l的方程为 :
: 易如:
易如:
设 ,
,


①M为AN中点 
由 (Ⅰ)、(Ⅱ)联解,得  代入(Ⅱ)
代入(Ⅱ)

 4
4
∴直线l的方程为 :  (7分)
(7分)
②
 (9分)
(9分)
FM为∠NFA的平分线
且
 (11分)
(11分)
又

 (14分)
(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com