
题目列表(包括答案和解析)
在科学研究中,可以通过施加适当的电场和磁场来实现对带电粒子运动的控制。如图所示的xOy平面处于匀强电场和匀强磁场中,电场强度E和磁感应强度B随时间t做周期性变化的图象如图所示。x 轴正方向为E的正方向,垂直纸面向里为B的正方向。在坐标原点O有一粒子P,其质量和电荷量分别为m和+q.不计重力。在t=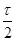 时刻释放P,它恰能沿一定轨道做往复运动。
时刻释放P,它恰能沿一定轨道做往复运动。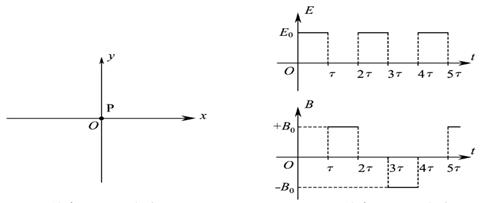
(1)求P在磁场中运动时速度的大小v0;
(2)求B0应满足的关系;
(3)在t0(0<t0<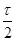 )时刻释放P,求P速度为零时的坐标。
)时刻释放P,求P速度为零时的坐标。
在科学研究中,可以通过施加适当的电场和磁场来实现对带电粒子运动的控制。如图所示的xOy平面处于匀强电场和匀强磁场中,电场强度E和磁感应强度B随时间t做周期性变化的图象如图所示。x 轴正方向为E的正方向,垂直纸面向里为B的正方向。在坐标原点O有一粒子P,其质量和电荷量分别为m和+q.不计重力。在t=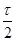 时刻释放P,它恰能沿一定轨道做往复运动。
时刻释放P,它恰能沿一定轨道做往复运动。
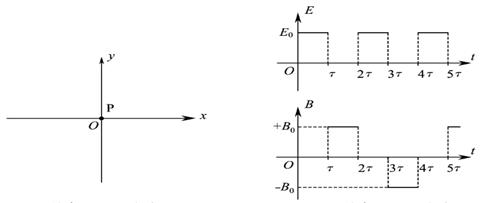
(1)求P在磁场中运动时速度的大小v0;
(2)求B0应满足的关系;
(3)在t0(0<t0<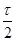 )时刻释放P,求P速度为零时的坐标。
)时刻释放P,求P速度为零时的坐标。
 时刻释放P,它恰能沿一定轨道做往复运动。
时刻释放P,它恰能沿一定轨道做往复运动。
 )时刻释放P,求P速度为零时的坐标。
)时刻释放P,求P速度为零时的坐标。 由于科学研究的需要,常常将质子p(
由于科学研究的需要,常常将质子p(| 1 |
| 1 |
| 4 |
| 2 |
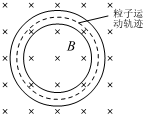 为了科学研究的需要,常常将带电粒子储存在圆环形状空腔中,圆环状空腔置于一个与圆环平面垂直的匀强磁场中,如图所示.如果磁场的磁感应强度为B,质子(
为了科学研究的需要,常常将带电粒子储存在圆环形状空腔中,圆环状空腔置于一个与圆环平面垂直的匀强磁场中,如图所示.如果磁场的磁感应强度为B,质子(1 1 |
4 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com