
题目列表(包括答案和解析)
(本小题满分12分)
第16届亚运会将于今年11月在我市举行,射击队运动员们正在积极备战. 若某运动员每次射击成绩为10环的概率为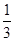 . 求该运动员在5次射击中,
. 求该运动员在5次射击中,
(1)恰有3次射击成绩为10环的概率;
(2)至少有3次射击成绩为10环的概率;
(3)射击成绩为10环的均值(数学期望).
(结果用分数表示)
(本小题满分12分)某射击运动员在一次射击中,命中10环、9环、8环、7环的概率分别为0.2、0.35、0.2、0.15。求此运动员
(1)在一次射击中,命中10环或9环的概率。
(2)在一次射击中,命中环数小于8环的概率。
(3)在两次射击中,至少有一次击中10环的概率。
(本小题满分12分)甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下:
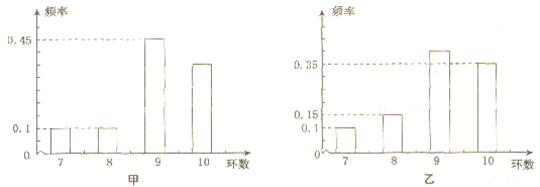
若将频率视为概率,回答下列问题.(Ⅰ)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率; (Ⅱ)若甲、乙两运动员各自射击1次,ξ表示这2次射击中击中9环以上(含9环)的次数,求ξ的分布列及Eξ.
(08年衡阳八中理) (12分) 甲、乙两名射击运动员,甲射击一次命中10环的概率为![]() ,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=
,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=![]() ,
,![]() 表示甲与乙命中10环的次数的差的绝对值.
表示甲与乙命中10环的次数的差的绝对值.
(1)求s的值及![]() 的分布列,
的分布列,
(2)求![]() 的数学期望.
的数学期望.
(本小题满分12分)
甲、乙两名射击运动员,甲射击一次命中10环的概率为![]() ,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=
,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=![]() ,
,![]() 表示甲与乙命中10环的次数的差的绝对值.
表示甲与乙命中10环的次数的差的绝对值.
(1)求s的值及![]() 的分布列, (2)求
的分布列, (2)求![]() 的数学期望.
的数学期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com