
题目列表(包括答案和解析)
| OP |
| i |
| j |
| k |
| i |
| j |
| k |
| OP |
| i |
| j |
| k |
| OP |
| j |
| OP |
| i |
| 1 |
| x |
| 2 |
| y |
| 2 |
| OP |
| i |
| j |
| k |
| OQ |
| i |
| j |
| k |
| PQ |
| k |
| PQ |
| OP |
| OM |
| i |
| j |
| k |
| OQ |
| i |
| j |
| k |
| OR |
| i |
| j |
| k |
| x |
| a |
| y |
| b |
| z |
| c |
| OP |
| i |
| j |
| k |
| OM |
| i |
| j |
| k |
| ON |
| i |
| j |
| k |
| PM |
| j |
| PN |
| j |
| PM |
| PN |
在空间直角坐标系O-xyz中,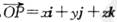 (其中i、j、k分别为X轴、y轴、z轴正方向上的单位向量).有下列命题:
(其中i、j、k分别为X轴、y轴、z轴正方向上的单位向量).有下列命题:
①若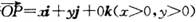 且
且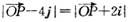 ,则
,则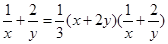
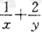 的最小值为
的最小值为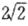 ;
;
②设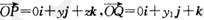 ,若向量
,若向量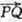 与k共线且
与k共线且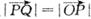 ,则动点P的轨迹是抛物线;
,则动点P的轨迹是抛物线;
③若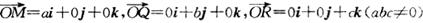 ,则平面MQR内的任意一点A (x,y,z)的坐标必然满足关系式
,则平面MQR内的任意一点A (x,y,z)的坐标必然满足关系式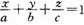 ;
;
④设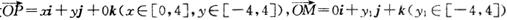 ,
,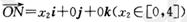 ,若向量
,若向量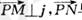 与j共线且
与j共线且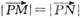 ,则动点P的轨迹是双曲线的一部分.
其中你认为正确的所有命题的序号为. _______
,则动点P的轨迹是双曲线的一部分.
其中你认为正确的所有命题的序号为. _______
在空间直角坐标系中,对其中任何一向量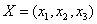 ,定义范数
,定义范数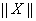 ,它满足以下性质:
,它满足以下性质:
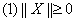 ,当且仅当
,当且仅当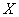 为零向量时,不等式取等号;
为零向量时,不等式取等号;
(2)对任意的实数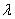 ,
,
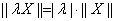 (注:此处点乘号为普通的乘号);
(注:此处点乘号为普通的乘号);
(3)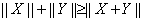 ;
;
试求解以下问题:在平面直角坐标系中,有向量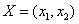 ,下面给出的几个表达式中,可能表示向量
,下面给出的几个表达式中,可能表示向量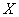 的范数的是____(把所有正确答案的序号都填上).
的范数的是____(把所有正确答案的序号都填上).
(1)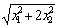 (2)
(2)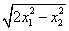 (3)
(3)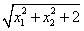 (4)
(4)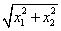
在空间直角坐标系中,对其中任何一向量![]() ,定义范数
,定义范数![]() ,它满足以下性质:
,它满足以下性质:![]() ,当且仅当
,当且仅当![]() 为零向量时,不等式取等号;(2)对任意的实数
为零向量时,不等式取等号;(2)对任意的实数![]() ,
,![]() (注:此处点乘号为普通的乘号)。(3)
(注:此处点乘号为普通的乘号)。(3)![]() 。试求解以下问题:在平面直角坐标系中,有向量
。试求解以下问题:在平面直角坐标系中,有向量![]() ,下面给出的几个表达式中,可能表示向量
,下面给出的几个表达式中,可能表示向量![]() 的范数的是_____ _______.(把所有正确答案的序号都填上)
的范数的是_____ _______.(把所有正确答案的序号都填上)
(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]()
 如图,空间直角坐标系O-xyz中,已知A(1,0,0),B(0,2,0),现将△AOB按向量
如图,空间直角坐标系O-xyz中,已知A(1,0,0),B(0,2,0),现将△AOB按向量| p |
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com