
题目列表(包括答案和解析)
已知数列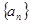 中,
中, ,点
,点 在直线
在直线 上,其中
上,其中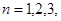 …。
…。
(1)令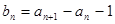 ,证明数列
,证明数列 是等比数列;
是等比数列;
(2)设 分别为数列
分别为数列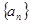 、
、 的前
的前 项和,证明数列
项和,证明数列 是等差数列。
是等差数列。
【解析】本试题主要考查了等差数列和等比数列的通项公式以及数列的求和的综合运用问题。既考查了概念,又考查了同学们的计算能力。
在递增等差数列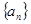 (
( )中,已知
)中,已知 ,
, 是
是 和
和 的等比中项.
的等比中项.
(1)求数列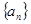 的通项公式;
的通项公式;
(2)设数列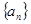 的前
的前 项和为
项和为 ,求使
,求使
 时
时 的最小值.
的最小值.
【解析】本试题主要考查了数列通项公式的求解以及前n项和公式的运用。并求解最值。
有四个数:前三个成等差数列,后三个成等比数列。首末两数和为16,中间两数和为12。求这四个数。
【解析】本试题主要是考查了等差数列和等比数列的通项公式的运用。
在等差数列{an}中,a1=3,其前n项和为Sn,等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+ S2=12,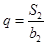 .(Ⅰ)求an 与bn;(Ⅱ)设数列{cn}满足
.(Ⅰ)求an 与bn;(Ⅱ)设数列{cn}满足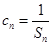 ,求{cn}的前n项和Tn.
,求{cn}的前n项和Tn.
【解析】本试题主要是考查了等比数列的通项公式和求和的运用。第一问中,利用等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+ S2=12,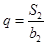 ,可得
,可得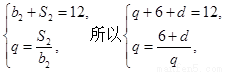 ,解得q=3或q=-4(舍),d=3.得到通项公式故an=3+3(n-1)=3n, bn=3 n-1. 第二问中,
,解得q=3或q=-4(舍),d=3.得到通项公式故an=3+3(n-1)=3n, bn=3 n-1. 第二问中,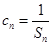 ,由第一问中知道
,由第一问中知道 ,然后利用裂项求和得到Tn.
,然后利用裂项求和得到Tn.
解: (Ⅰ) 设:{an}的公差为d,
因为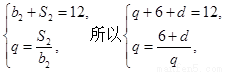 解得q=3或q=-4(舍),d=3.
解得q=3或q=-4(舍),d=3.
故an=3+3(n-1)=3n, bn=3 n-1. ………6分
(Ⅱ)因为 ……………8分
……………8分
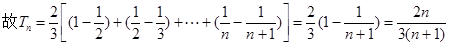
已知递增等差数列 满足:
满足: ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式
的通项公式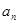 ;
;
(2)若不等式 对任意
对任意 恒成立,试猜想出实数
恒成立,试猜想出实数 的最小值,并证明.
的最小值,并证明.
【解析】本试题主要考查了数列的通项公式的运用以及数列求和的运用。第一问中,利用设数列 公差为
公差为 ,
,
由题意可知 ,即
,即 ,解得d,得到通项公式,第二问中,不等式等价于
,解得d,得到通项公式,第二问中,不等式等价于 ,利用当
,利用当 时,
时, ;当
;当 时,
时, ;而
;而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 然后加以证明即可。
然后加以证明即可。
解:(1)设数列 公差为
公差为 ,由题意可知
,由题意可知 ,即
,即 ,
,
解得 或
或 (舍去). …………3分
(舍去). …………3分
所以, . …………6分
. …………6分
(2)不等式等价于 ,
,
当 时,
时, ;当
;当 时,
时, ;
;
而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 . …………8分
. …………8分
下证不等式 对任意
对任意 恒成立.
恒成立.
方法一:数学归纳法.
当 时,
时, ,成立.
,成立.
假设当 时,不等式
时,不等式 成立,
成立,
当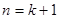 时,
时, ,
…………10分
,
…………10分
只要证  ,只要证
,只要证  ,
,
只要证  ,只要证
,只要证  ,
,
只要证  ,显然成立.所以,对任意
,显然成立.所以,对任意 ,不等式
,不等式 恒成立.…14分
恒成立.…14分
方法二:单调性证明.
要证 
只要证  ,
,
设数列 的通项公式
的通项公式 , …………10分
, …………10分
 , …………12分
, …………12分
所以对 ,都有
,都有 ,可知数列
,可知数列 为单调递减数列.
为单调递减数列.
而 ,所以
,所以 恒成立,
恒成立,
故 的最小值为
的最小值为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com