
题目列表(包括答案和解析)
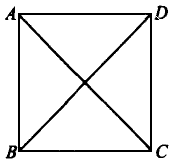
已知:如图,在四边形ABCD中,∠ACD=∠DAC=∠ADB=∠ABD=![]() .
.
求证:四边形ABCD是正方形.
在研究“三角形的三个内角和等于180°”的证明方法时,小明和小虎分别给出了下列证法:
小明:在△ABC中,延长BC到点D(如图),
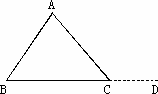
所以∠ACD=∠A+∠B.(三角形的一个外角等于与它不相邻的两个内角的和)
又因为∠ACD+∠ACB=180°,(平角定义)
所以∠A+∠B+∠ACB=180°.(等量代换)
小虎:在△ABC中,过点A作AD⊥BC(如图),

所以∠ADC=∠ADB=90°.(直角定义)
所以∠DAC+∠C=90°,∠B+∠BAD=90°.(直角三角形的两锐角互余)
所以∠DAC+∠C+∠B+∠BAD=180°,
即∠BAC+∠B+∠C=180°.
请你对上述两名同学的证法给出评价,并写出一种你认为较简单的证明三角形内角和定理的方法.
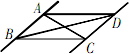
如图,给出下列四个条件:①AC=BD;②∠DAC=∠BCA;③∠ABD=∠CDB;④∠ADB=∠CBD.
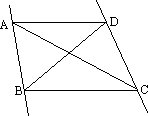
其中能使AD∥BC的条件有
[ ]
如图,AC是某市坏城路的一段,AE、BF、CD都是南北方向的街道,其与环城路AC的交叉路口分别是A、B、C经测量花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2 km,∠DAC=15°.
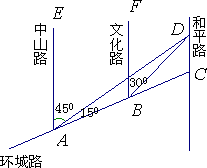
(1)求∠ADB的大小;
(2)求B、D之间的距离;
(3)求C、D之间的距离.
如图,给出下列四个条件:①AC=BD;②∠DAC=∠BCA;③∠ABD=∠CDB;④∠ADB=∠CBD,其中能使AD∥BC的条件是
①②
③④
②④
①③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com