（01上海卷）（10分）如图A所示，一质量为m的物体系于长度分别为l₁、l₂的两根细线上，l₁的一端悬挂在天花板上，与竖直方向夹角为θ，l₂水平拉直，物体处于平衡状态。现将l₂线剪断，求剪断瞬时物体的加速度。

（l）下面是某同学对该题的一种解法：

解：设l₁线上拉力为T₁，线上拉力为T_2，重力为mg，物体在三力作用下保持平衡

T₁cosθ＝mg，   T₁sinθ＝T₂，  T₂＝mgtgθ

剪断线的瞬间，T₂突然消失，物体即在T₂反方向获得加速度。因为mg tgθ＝ma，所以加速度a＝g tgθ，方向在T₂反方向。

你认为这个结果正确吗？请对该解法作出评价并说明理由。

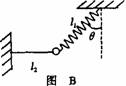
（2）若将图A中的细线l₁改为长度相同、质量不计的轻弹簧，如图B所示，其他条件不变，求解的步骤和结果与（l）完全相同，即 a＝g tgθ，你认为这个结果正确吗？请说明理由。

（01年上海卷）（10分）如图A所示，一质量为m的物体系于长度分别为l₁、l₂的两根细线上，l₁的一端悬挂在天花板上，与竖直方向夹角为θ，l₂水平拉直，物体处于平衡状态。现将l₂线剪断，求剪断瞬时物体的加速度。

（l）下面是某同学对该题的一种解法：

解：设l₁线上拉力为T₁，线上拉力为T_2，重力为mg，物体在三力作用下保持平衡

T₁cosθ＝mg，   T₁sinθ＝T₂，  T₂＝mgtgθ

剪断线的瞬间，T₂突然消失，物体即在T₂反方向获得加速度。因为mg tgθ＝ma，所以加速度a＝g tgθ，方向在T₂反方向。

你认为这个结果正确吗？请对该解法作出评价并说明理由。

（2）若将图A中的细线l₁改为长度相同、质量不计的轻弹簧，如图B所示，其他条件不变，求解的步骤和结果与（l）完全相同，即 a＝g tgθ，你认为这个结果正确吗？请说明理由。

（01年上海卷）（18分）如图所示，光滑斜面的底端a与一块质量均匀、水平放置的平极光滑相接，平板长为2L，L＝1m，其中心C固定在高为R的竖直支架上，R＝1m，支架的下端与垂直于纸面的固定转轴O连接，因此平板可绕转轴O沿顺时针方向翻转。问：

（1）在外面上离平板高度为h₀处放置一滑块A，使其由静止滑下，滑块与平板间的动摩擦因数μ＝0.2，为使平板不翻转，h₀最大为多少？

（2）如果斜面上的滑块离平板的高度为h₁＝0.45 m，并在h₁处先后由静止释放两块质量相同的滑块A、B，时间间隔为Δt＝0.2s，则B滑块滑上平板后多少时间，平板恰好翻转。（重力加速度g取10 m/s²）

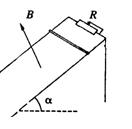
（01年上海卷）如图所示，有两根和水平方向成α角的光滑平行的金属轨道，上端接有可变电阻R，下端足够长，空间有垂直于轨道平面的匀强磁场，磁感强度为B,一根质量为m的金属杆从轨道上由静止滑下。经过足够长的时间后，金属杆的速度会趋近于一个最大速度，则

（A）如果B增大，v_m将变大

（B）如果α变大，v_m将变大

（C）如果R变大，v_m将变大

（D）如果m变小，v_m将变大

（01年上海卷）如图所示，有两根和水平方向成。角的光滑平行的金属轨道，上端接有可变电阻R，下端足够长，空间有垂直于轨道平面的匀强磁场，磁感强度为及一根质量为m的金属杆从轨道上由静止滑下。经过足够长的时间后，金属杆的速度会趋近于一个最大速度，则

（A）如果B增大，v_m将变大

（B）如果α变大，v_m将变大

（C）如果R变大，v_m将变大

（D）如果m变小，v_m将变大