题目列表(包括答案和解析)
（本小题满分12分）二次函数
的图象经过三点
.
（1）求函数的解析式（2）求函数在区间
上的最大值和最小值
（本小题满分12分）已知等比数列{an}中，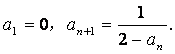
（Ⅰ）求数列{an}的通项公式an；
（Ⅱ）设数列{an}的前n项和为Sn，证明:
；
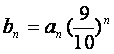，证明：对任意的正整数n、m，均有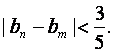
（本小题满分12分）已知函数
，其中a为常数.
（Ⅰ）若当
恒成立，求a的取值范围；
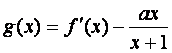的单调区间.（本小题满分12分）
甲、乙两篮球运动员进行定点投篮，每人各投4个球，甲投篮命中的概率为
，乙投篮命中的概率为
（Ⅰ）求甲至多命中2个且乙至少命中2个的概率；
（Ⅱ）若规定每投篮一次命中得3分，未命中得－1分，求乙所得分数η的概率分布和数学期望.（本小题满分12分）已知
是椭圆
的两个焦点，O为坐标原点，点
在椭圆上，且
，圆O是以
为直径的圆，直线
与圆O相切，并且与椭圆交于不同的两点A、B.
（1）求椭圆的标准方程；w.w.w.k.s.5.u.c.o.m 
（2）当
时，求弦长|AB|的取值范围.
一、选择题：
ADBAA BCCDC
二、填空题：
11． 
； 12． 
； 13．
14（i） ③⑤ （ii） ②⑤ 15．（i）7; （ii）
.
三、解答题：
16.解：（Ⅰ）
…………5分
由
成等比数列，知
不是最大边
…………6分
（Ⅱ）由余弦定理
得ac=2 …………11分
=
…………12分
17．解：（Ⅰ）第一天通过检查的概率为
，
………………………２分
第二天通过检查的概率为
，
…………………………４分
由相互独立事件得两天全部通过检查的概率为
． ………………６分
（Ⅱ）第一天通过而第二天不通过检查的概率为
， …………８分
第二天通过而第一天不通过检查的概率为
，
………………10分
由互斥事件得恰有一天通过检查的概率为
． ……………………12分
18．解：方法一
（Ⅰ）取
的中点
，连结
，由
知
，又
，故
，所以
即为二面角
的平面角.
在△
中，
，
，
，
由余弦定理有
，
所以二面角的大小是
.
（6分）
（Ⅱ）由（Ⅰ）知道
平面，故平面
平面，故
在平面
上的射影一定在直线上，所以点到平面
的距离即为△的边上的高.
故
.
…（12分）
19．解：（Ⅰ）设
则 
……①
……②
∴②－①得 2d2=0，∴d=p=0
∴
…………6分
（Ⅱ）当an=n时，恒等式为[S（1，n）]2=S（3，n）
证明：
相减得： 
∴
相减得：
又
又
∴
………………………………13分
20．解：（Ⅰ）∵
，∴
，
又∵
，∴
，
∴
，
∴椭圆的标准方程为
．
………（3分）
当
的斜率为0时，显然
=0，满足题意，
当的斜率不为0时，设方程为
，
代入椭圆方程整理得：
．
，
，
．
则
，
而
∴
，从而．
综合可知：对于任意的割线
，恒有．
………（8分）
（Ⅱ）
，
即：
，
当且仅当
，即
（此时适合于
的条件）取到等号．
∴三角形△ABF面积的最大值是
． ………………………………（13分）
21．解：（Ⅰ）
……………………………………………4分
（Ⅱ）
或者
……………………………………………8分
（Ⅲ）略 ……………………………………13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com