练习册

  • 练习册
  • 试题
    用一根细线一端系一小球.另一端固定在一光滑圆锥顶上. 如图4所示．设小球在水平面内做匀速圆周运动的角速度为ω.线的张力 为FT.则FT随ω2变化的图象是图5中的 ( ) 图4 图5 解析:小球角速度ω较小.未离开锥面时.设线的张力为FT.线的长度为L.锥面对小球的支持力为FN.则有FTcosθ+FNsinθ＝mg.FTsinθ-FNcosθ＝mω2Lsinθ.可得出:FT＝mgcosθ+mω2Lsin2θ.可见随ω由0开始增加.FT由mgcosθ开始随ω2的增大.线性增大.当角速度增大到小球飘离锥面时.FT·sinα＝mω2Lsinα.得FT＝mω2L.可见FT随ω2的增大仍线性增大.但图线斜率增大了.综上所述.只有C正确． 答案:C 【查看更多】

     

    题目列表(包括答案和解析)

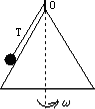
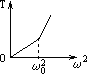
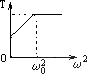
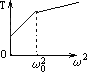
    用一根细线一端系一小球(可视为质点)，另一端固定在一光滑圆锥顶上，  如图4所示．设小球在水平面内做匀速圆周运动的角速度为ω，线的张力为FT，则FT随ω2变化的图象是图5中的                     (　　)   

     

    查看答案和解析>>

    用一根细线一端系一小球(可视为质点)，另  一端固定在一光滑锥顶上，如图所示，设小球在水平面内做匀速圆周运动的角速度为ω，细线的张力为FT，则FT随ω2变化的图象是
    [     ]
    A.
    B.
    C.
    D.

    查看答案和解析>>

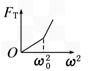
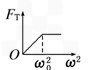
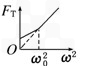
    用一根细线一端系一小球(可视为质点)，另一端固定在一光滑圆锥顶上， 如图4所示．设小球在水平面内做匀速圆周运动的角速度为ω，线的张力为FT，则FT随ω2变化的图象是图5中的                     (　　)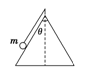   

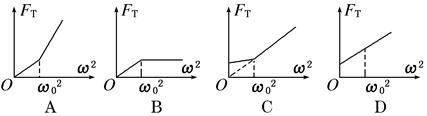
    查看答案和解析>>

    用一根细线一端系一小球(可视为质点)，另一端固定在一光滑圆锥顶上， 如图所示．设小球在水平面内做匀速圆周运动的角速度为ω，线的张力为FT，则FT随ω2变化的图象是图中的                     (　　)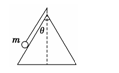      

    查看答案和解析>>

    用一根细线一端系一小球(可视为质点)，另一端固定在一光滑圆锥顶上，如下图所示，设小球在水平面内作匀速圆周运动的角速度为ω，线的张力为T，则T随ω2变化的图象是下图中的

    A．

    B．

    C．

    D．

    查看答案和解析>>


    同步练习册答案