
题目列表(包括答案和解析)
| 1 |
| x |
| 1 |
| x |
| f(x)2-2x |
| 2 |
| s2 |
| 2 |
| s3 |
| 3 |
| sn |
| n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2 |
 )=1;(3)对M中的任意x1、x2都有f=f(x1)+f(x2);(4)y=f(x)在M上的反函数为y=f-1(x).
)=1;(3)对M中的任意x1、x2都有f=f(x1)+f(x2);(4)y=f(x)在M上的反函数为y=f-1(x). ∈M,但
∈M,但 ∉M;
∉M; .
.(本题18分)在R+上的递减函数f(x)同时满足:(1)当且仅当xÎM ![]() R+时,函数值f(x)的集合为[0, 2];(2)f(
R+时,函数值f(x)的集合为[0, 2];(2)f(![]() )=1;(3)对M中的任意x1、x2都有f(x1•x2)= f(x1)+ f(x2);(4)y=f(x)在M上的反函数为y=f–1(x).
)=1;(3)对M中的任意x1、x2都有f(x1•x2)= f(x1)+ f(x2);(4)y=f(x)在M上的反函数为y=f–1(x).
(1)求证:![]() ÎM,但
ÎM,但![]() ÏM;
ÏM;
(2)求证:f–1(x1)• f–1(x2)= f–1(x1+x2);
(3)解不等式:f–1(x2–x)• f–1(x–1)≤![]() .
.
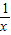 )=2x+
)=2x+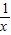 +3.
+3. (x≥0)直线 y=
(x≥0)直线 y=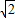 n-x分别与函数f(x) 的反函数 交于A,B两点
n-x分别与函数f(x) 的反函数 交于A,B两点 )成立.
)成立.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com