
题目列表(包括答案和解析)
(17) (本小题满分10分)(注意:在试题卷上作答无效)
设等差数列{![]() }的前
}的前![]() 项和为
项和为![]() ,公比是正数的等比数列{
,公比是正数的等比数列{![]() }的前
}的前![]() 项和为
项和为![]() ,
,
已知![]() 的通项公式.
的通项公式.
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)
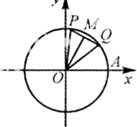
如图,P,Q是以原点为圆心的单位圆上的两个动点,若它们同时从点A(1,0)出发,沿逆时针方向作匀角速度运动,其角速度分别为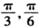 (单位:弧度/秒),M为线段PQ的中点,记经过x秒后(其中
(单位:弧度/秒),M为线段PQ的中点,记经过x秒后(其中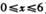 ),
),
(I)求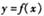 的函数解析式;
的函数解析式;
(II)将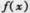 图象上的各点均向右平移2个单位长度,得到
图象上的各点均向右平移2个单位长度,得到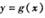 的图象,求函数
的图象,求函数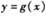 的单调递减区间.
的单调递减区间.
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17. (本小题满分10分)
已知复数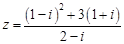 ,若
,若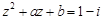 ,
,
⑴求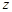 ;
;
⑵求实数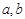 的值
的值
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)
设向量 ,向量
,向量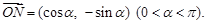
(1)若向量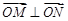 ,求
,求 的值;
的值;
(2)求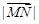 的最大值及此时
的最大值及此时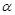 的值。
的值。
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)
设向量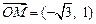 ,向量
,向量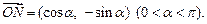
(1)若向量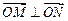 ,求
,求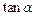 的值;
的值;
(2)求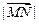 的最大值及此时
的最大值及此时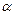 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com