
题目列表(包括答案和解析)
已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1
(1) 求曲线C的方程.
(2) 是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有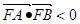 ?若存在,求出m的取值范围,若不存在,请说明理由.
?若存在,求出m的取值范围,若不存在,请说明理由.
【解析】(1)由题意知曲线C上的点到F(1,0)的距离与到直线x=-1的距离相等.
可确定其轨迹是抛物线,即可求出其方程为y2=4x.
(2)设过点M的直线方程为x=ty+m,然后与抛物线方程联立,消去x,利用韦达定理表示出 ,再证明其小于零即可.
,再证明其小于零即可.
在△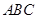 中,∠
中,∠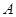 ,∠
,∠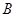 ,∠
,∠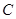 的对边分别是
的对边分别是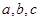 ,且
,且
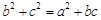 .
.
(1)求∠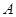 的大小;(2)若
的大小;(2)若 ,
,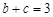 ,求
,求 和
和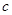 的值.
的值.
【解析】第一问利用余弦定理得到
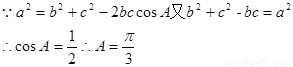 第二问
第二问
(2) 由条件可得 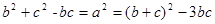
将  代入 得 bc=2
代入 得 bc=2
解得 b=1,c=2 或 b=2,c=1 .
已知△ABC的三个内角A、B、C所对的边分别为a、b、c,向量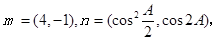
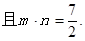
(Ⅰ)求角A的大小;
(Ⅱ)若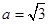 ,试判断b·c取得最大值时△ABC形状.
,试判断b·c取得最大值时△ABC形状.
【解析】本试题主要考查了解三角形的运用。第一问中利用向量的数量积公式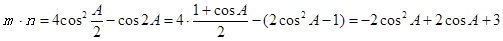 ,且由
,且由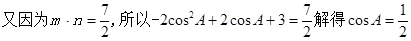
(2)问中利用余弦定理 ,以及
,以及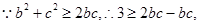 ,可知
,可知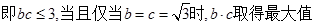 ,并为等边三角形。
,并为等边三角形。
解:(Ⅰ)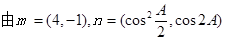
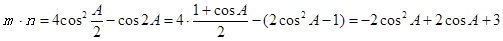
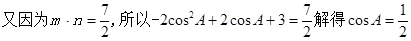
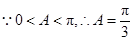 ………………………………6分
………………………………6分
(Ⅱ)
 ………………………………8分
………………………………8分
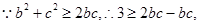
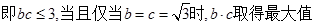 ……………10分
……………10分

设A是如下形式的2行3列的数表,
|
a |
b |
c |
|
d |
e |
f |
满足性质P:a,b,c,d,e,f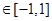 ,且a+b+c+d+e+f=0
,且a+b+c+d+e+f=0
记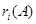 为A的第i行各数之和(i=1,2),
为A的第i行各数之和(i=1,2),  为A的第j列各数之和(j=1,2,3)记
为A的第j列各数之和(j=1,2,3)记 为
为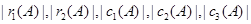 中的最小值。
中的最小值。
(1)对如下表A,求 的值
的值
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
(2)设数表A形如
|
1 |
1 |
-1-2d |
|
d |
d |
-1 |
其中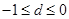 ,求
,求 的最大值
的最大值
(3)对所有满足性质P的2行3列的数表A,求 的最大值。
的最大值。
【解析】(1)因为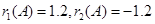 ,
,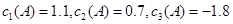 ,所以
,所以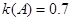
(2)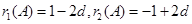 ,
,
因为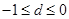 ,所以
,所以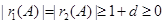 ,
,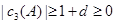
所以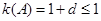
当d=0时, 取得最大值1
取得最大值1
(3)任给满足性质P的数表A(如图所示)
|
a |
b |
c |
|
d |
e |
f |
任意改变A的行次序或列次序,或把A中的每个数换成它的相反数,所得数表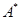 仍满足性质P,并且
仍满足性质P,并且 ,因此,不妨设
,因此,不妨设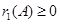 ,
, ,
,
由 得定义知,
得定义知,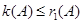 ,
,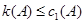 ,
,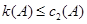 ,
,
从而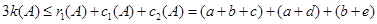
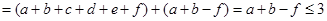
所以, ,由(2)知,存在满足性质P的数表A使
,由(2)知,存在满足性质P的数表A使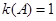 ,故
,故 的最大值为1
的最大值为1
【考点定位】此题作为压轴题难度较大,考查学生分析问题解决问题的能力,考查学生严谨的逻辑思维能力
| a |
| 1 |
| x |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com