
题目列表(包括答案和解析)
答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、班级和考号填写在答题卷上。
已知A、B两地的路程为240千米.某经销商每天都要用汽车或火车将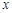 吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时)的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:
货运收费项目及收费标准表
|
运输工具 |
运输费单价:元/(吨?千米) |
冷藏费单价:元/(吨?时) |
固定费用:元/次 |
|
汽车 |
2 |
5 |
200 |
|
火车 |
1.6 |
5 |
2280 |
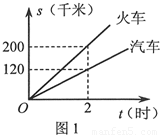
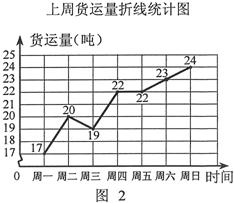
(1)汽车的速度为 千米/时,火车的速度为 千米/时:
(2)设每天用汽车和火车运输的总费用分别为 汽(元)和
汽(元)和 火(元),分别求
火(元),分别求 汽、
汽、 火与
火与 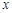 的函数关系式(不必写出
的函数关系式(不必写出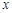 的取值范围),及
的取值范围),及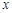 为何值时
为何值时 汽>
汽> 火(总费用=运输费+冷藏费+固定费用)
火(总费用=运输费+冷藏费+固定费用)
(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前为下周预定哪种运输工具,才能使每天的运输总费用较省?
| 2 | 3 |
 ,且各题之间答对与否互不影响.已知该选手已经答对前6道题.
,且各题之间答对与否互不影响.已知该选手已经答对前6道题.
一、选择题(本大题共8小题,每小题5分,共40分)
题号
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
答案
(D)
(B)
(A)
(A)
(D)
(C)
(B)
(C)
二、填空题(本大题共6小题,每小题5分.有两空的小题,第一空3分,第二空2分,共30分)
(9)-1 (10){x|x<-4,或x>-1} (11)4
(12)(0,-1),(x-1)2+(y-1)2=1 (13).files/image049.gif) (14)4,8
(14)4,8
三、解答题(本大题共6小题,共80分)
(15)(共12分)
解:(Ⅰ)∵p =(sinx,cosx+sinx), q =(2cosx,cosx-sinx),
∴f(x)=p?q=(sinx,cosx+sinx)?(2cosx,cosx-sinx)
=2sinxcosx+cos2x-sin2x …………………………………… 2分
=sin2x+cos2x ………………………………………………
4分
∴ f(.files/image006.gif) )=
)=.files/image089.gif) . ……………………………………………………
5分
. ……………………………………………………
5分
又f(x)=sin2x+cos2x=.files/image049.gif) sin(2x+
sin(2x+.files/image075.gif) ) ……………………………
6分
) ……………………………
6分
∴函数f(x)的最大值为.files/image049.gif) . ………………………………………
7分
. ………………………………………
7分
当且仅当x=.files/image092.gif) +k
+k.files/image094.gif) (k
(k.files/image044.gif) Z)时,函数f(x)取得最大值
Z)时,函数f(x)取得最大值.files/image049.gif) .
.
(Ⅱ)由2k.files/image094.gif) -
-.files/image098.gif) ≤2x+
≤2x+.files/image075.gif) ≤2k
≤2k.files/image094.gif) +
+.files/image098.gif) ( k
( k.files/image044.gif) Z), ……………………
9分
Z), ……………………
9分
得k.files/image094.gif) -
-.files/image100.gif) ≤x≤k
≤x≤k.files/image094.gif) +
+.files/image092.gif) . …………………………………………
11分
. …………………………………………
11分
函数f(x)的单调递增区间为[k.files/image094.gif) -
-.files/image100.gif) , k
, k.files/image094.gif) +
+.files/image092.gif) ](
k
](
k.files/image044.gif) Z). ……
12分
Z). ……
12分
(16)(共14分)
解法一:(Ⅰ)证明:连结A1D,在正方体AC1中,∵A1B1⊥平面A1ADD1,
∴A1D是PD在平面A1ADD1内的射影. …………………………………… 2分
∵在正方形A1ADD1中,A1D⊥AD1,∴PD⊥AD1. ……………………… 4分
解:(Ⅱ)取D
∵A1D1⊥平面D1DCC1,∴PM⊥平面D1DCC1.
∴CM为CP在平面D1DCC1内的射影.则∠PCM为CP与平面D1DCC1
所成的角. …………………………………………………………… 7分
在Rt△PCM中,sinPCM=.files/image102.gif) =
=.files/image104.gif) .
.
∴CP与平面D1DCC1所成角的正弦值为.files/image106.gif) . …………………………… 9分
. …………………………… 9分
.files/image108.jpg) (Ⅲ)在正方体AC1中,D1D∥C
(Ⅲ)在正方体AC1中,D1D∥C
∵C.files/image110.gif) 平面D1DP内,
平面D1DP内,
∴C
∴点C到平面D1DP的距离与点C1
到平面D1DP的距离相等.
又D1D⊥平面A1B
DD1.files/image030.gif) 平面D1DP
平面D1DP
∴平面D1DP⊥平面A1B
又平面D1DP∩平面A1B
D1P,过C1作C1H⊥D1P于H,
则C1H⊥平面D1DP.
∴C1H的长为点C1到平面D1DP的距离. ………………………12分
连结C1P,并在D
C1H?D1P=PQ?D.files/image113.gif) .
.
∴点C到平面D1DP的距离为.files/image115.gif) . ………………………………
14分
. ………………………………
14分
解法二:如图,以D为坐标原点,建立空
.files/image117.jpg) 间直角坐标系D-xyz.
间直角坐标系D-xyz.
由题设知正方体棱长为4,则
D(0,0,0) ,A(4,0,0),
B1(4,4,4) ,A1(4,0,4),
D1(0,0,4) ,C(0,4,0).
………………………………………1分
(Ⅰ)设P(4,y0,4),
∴.files/image119.jpg) =(4,y0,4),
=(4,y0,4),
∴.files/image121.jpg) =(-4,0,4)
=(-4,0,4)
……………………………3分
∵.files/image122.jpg) ?
?.files/image123.jpg) =-16+16=0,
=-16+16=0,
∴PD⊥AD1. …………………………………………………………… 4分
(Ⅱ)由题设可得,P(4,2,4),故.files/image125.jpg) =(4,-2,4).
=(4,-2,4).
∵AD⊥平面D1DCC1, ∴.files/image127.jpg) =(4,0,0)是平面D1DCC1的法向量. ……………
=(4,0,0)是平面D1DCC1的法向量. ……………
……………………………………………………………………………… 7分
.files/image129.jpg) ∴cos<
∴cos<.files/image127.jpg) ,
,
.files/image125.jpg) >=
=
>=
=.files/image106.gif) .……………………………………………… 8分
.……………………………………………… 8分
∴CP与平面D1DCC1所成角的正弦值为.files/image106.gif) . …………………………………… 9分
. …………………………………… 9分
(Ⅲ) ∵.files/image132.jpg) =(0,4,0),设平面D1DP的法向量n=(x,y,z),
=(0,4,0),设平面D1DP的法向量n=(x,y,z),
∵P(4,3,4), ∴.files/image134.jpg) =(0,0,4),
=(0,0,4),.files/image119.jpg) =(4,3,4).
=(4,3,4).
.files/image136.jpg) 则
即
则
即.files/image138.gif) 令x=-3,则y=4.
令x=-3,则y=4.
∴n=(-3,4,0). ……………………………………………………………… 12分
.files/image140.jpg) ∴点C到平面D1DP的距离为d= =
∴点C到平面D1DP的距离为d= =.files/image115.gif) . ………………………… 14分
. ………………………… 14分
(17)(共13分)
解:(Ⅰ)设事件“某人参加A种竞猜活动只获得一个福娃奖品”为事件M,…… 1分
依题意,答对一题的概率为.files/image067.gif) ,则
,则
P(M)=.files/image142.gif) …………………………………………………… 3分
…………………………………………………… 3分
=15×.files/image144.gif) =
=.files/image146.gif) =
=.files/image148.gif) . ………………………………………………… 4分
. ………………………………………………… 4分
(Ⅱ)依题意,某人参加B种竞猜活动,结束时答题数η=1,2,…,6,……… 5分
则P(η=1)=.files/image067.gif) ,P(η=2)=
,P(η=2)=.files/image151.gif) ,P(η=3)=
,P(η=3)=.files/image153.gif) ,P(η=4)=
,P(η=4)=.files/image155.gif) , P(η=5)=
, P(η=5)=.files/image157.gif) ,
,
P(η=6)= .files/image159.gif) , ……………………………………………………… 11分
, ……………………………………………………… 11分
所以,η的分布列是
η
1
2
3
4
5
6
.files/image067.gif)
.files/image151.gif)
.files/image153.gif)
.files/image155.gif)
.files/image157.gif)
.files/image159.gif)
Eη=1×.files/image163.gif) +2×
+2×.files/image165.gif) ×
×.files/image163.gif) +…+5×
+…+5×.files/image167.gif) ×
×.files/image163.gif) +6×
+6×.files/image169.gif) .
.
设S=1+2×.files/image165.gif) +…+5×
+…+5×.files/image167.gif) ,
,
则.files/image165.gif) S=
S=.files/image165.gif) +2×
+2×.files/image172.gif) +3×
+3×.files/image174.gif) +4×
+4×.files/image167.gif) +5×
+5×.files/image169.gif) ,
,
.files/image163.gif) S=1+
S=1+.files/image165.gif) +
+.files/image172.gif) +
+.files/image174.gif) +
+.files/image177.gif) -5×
-5×.files/image179.gif) =
=.files/image181.gif) -5×
-5×.files/image169.gif) ,
,
Eη=.files/image181.gif) -5×
-5×.files/image169.gif) +6×
+6×.files/image169.gif) =
=.files/image184.gif) =
=.files/image186.gif) . ………………………
13分
. ………………………
13分
答:某人参加A种竞猜活动只获得一个福娃奖品的概率为.files/image148.gif) ;某人参加B种竞猜活动,
;某人参加B种竞猜活动,
结束时答题数为η,Eη为.files/image186.gif) .
.
(18)(共13分)
.files/image189.jpg) 解:如图,建立直角坐标系,依题意:设
解:如图,建立直角坐标系,依题意:设
椭圆方程为.files/image191.gif) +
+.files/image193.gif) =1(a>b>0),
=1(a>b>0),
……………………………… 1分
(Ⅰ)依题意:.files/image195.gif) =
=.files/image197.gif) ,b=1,
,b=1,
a2= b2+c2, ………… 4分
∵椭圆M的离心率大于0.7,
∴a2=4, b2=1.
∴椭圆方程为.files/image199.gif) +y2=1. ……………………………………………………
6分
+y2=1. ……………………………………………………
6分
(Ⅱ)因为直线l过原点与椭圆交于点P,Q,设椭圆M的左焦点为F1.由对称性可知,
四边形PF1QF2是平行四边形.
∴△PF2Q的面积等于△PF
∵∠PF2Q=.files/image008.gif) ,∴∠F1PF2=
,∴∠F1PF2=.files/image006.gif) .
.
设|PF1|=r1,
|PF2|=r2,则.files/image203.gif) ………………………………
10分
………………………………
10分
∴r1
r2=.files/image205.gif) . …………………………………………………………………
11分
. …………………………………………………………………
11分
∴S△.files/image207.gif) =S△
=S△.files/image209.gif) =
= .files/image211.gif) r1 r2sin
r1 r2sin.files/image006.gif) =
=.files/image213.gif) . …………………………………
13分
. …………………………………
13分
(19)(共14分)
解:(Ⅰ)f′(x)=-3x2+2ax. ……………………………………………………… 1分
据题意,f′(1)=tan.files/image075.gif) =1, ∴-3+2a=1,即a=2.
……………………………3分
=1, ∴-3+2a=1,即a=2.
……………………………3分
(Ⅱ)由(Ⅰ)知f(x)=-x3+2x2-4,
则f′(x)=-3x2+4x.
x
-1
(-1,0)
0
(0,1)
1
f′(x)
-7
-
0
+
1
f(x)
-1
.files/image216.jpg)
-4
.files/image218.jpg)
-3
…………………………………………………………………………… 5分
∴对于m.files/image044.gif) [-1,1],f(m)的最小值为f(0)=-4 …………………
6分
[-1,1],f(m)的最小值为f(0)=-4 …………………
6分
∵f′( x)=-3x2+4x的对称轴为x=.files/image221.gif) ,且抛物线开口向下,
,且抛物线开口向下,
∴x.files/image044.gif) [-1,1]时,f′( x)的最小值为f′( -1)与f′( 1)中较小的.
[-1,1]时,f′( x)的最小值为f′( -1)与f′( 1)中较小的.
∵f′( 1)=1,f′( -1)=-7,
∴当x.files/image044.gif) [-1,1]时,f′( x)的最小值为-7.
[-1,1]时,f′( x)的最小值为-7.
∴当n.files/image044.gif) [-1,1]时,f′ ( x)的最小值为-7. ……………………
7分
[-1,1]时,f′ ( x)的最小值为-7. ……………………
7分
∴f(m)+ f′( n)的最小值为-11. ………………………………… 8分
(Ⅲ) ∵f′( x)= -3x.files/image223.gif) .
.
①若a≤0,当x>0时,f′( x)<0, ∴f(x)在[0,+∞.files/image225.jpg) 上单调递减.
上单调递减.
又f(0)=-4,则当x>0时,f(x)<-4.
∴当a≤0时,不存在x0>0,使f(x0)>0. …………………………………… 11分
②若a>0,则当0<x<.files/image227.gif) 时,f ′( x)>0,当x>
时,f ′( x)>0,当x>.files/image227.gif) 时,f ′( x)<0.
时,f ′( x)<0.
从而f(x)在(0, .files/image227.gif)
.files/image229.jpg) 上单调递增,在 [
上单调递增,在 [.files/image227.gif) ,+∞
,+∞.files/image231.gif) 上单调递减.
上单调递减.
∴当x.files/image044.gif) (0,+∞)时,
f(x)max=f(
(0,+∞)时,
f(x)max=f(.files/image234.gif) )=-
)=-.files/image236.gif) +
+.files/image238.gif) -4=
-4=.files/image240.gif) -4.
-4.
据题意,.files/image240.gif) -4>0,即a3>27.
∴a>3. ………………………………
14分
-4>0,即a3>27.
∴a>3. ………………………………
14分
综上,a的取值范围是(3,+∞).
(20)(共14分)
解:(Ⅰ)由①知,对任意a,b.files/image044.gif) N*,a<b,都有(a
N*,a<b,都有(a.files/image243.gif) b)(f (a)
b)(f (a).files/image243.gif) f(b))>0,
f(b))>0,
由于a-b<0, 从而f(a)<f(b),所以函数f(x)为N*上的单调增函数. …3分
(Ⅱ)令f(1)=a,则a≥1,显然a≠1,否则f(f(1))= f(1)=1,与f(f(1))=3矛盾.
从而a>1,
而由f(f(1))=3,即得f(a)=3.
又由(Ⅰ)知f(a)>f(1)=a ,即a<3.
于是得1<a<3,又a.files/image044.gif) N*,从而a=2,即f(1)=2 ……………… 5分
N*,从而a=2,即f(1)=2 ……………… 5分
进而由f(a)=3知,f(2)=3.
于是f(3)=f(f(2))=3×2=6,………………………………… 7分
f(6)=f(f(3))=3×3=9,
f(9)=f(f(6))=3×6=18,
f(18)=f(f(9))=3×9=27,
f(27)=f(f(18))=3×18=54,
f(54)=f(f(27))=3×27=81.
由于54.files/image243.gif) 27=81
27=81.files/image243.gif) 54=27,
54=27,
而且由(Ⅰ)知,函数f(x)为单调增函数,因此f(28)=54+1=55.
从而f(1)+f(6)+f(28)=2+9+55=66.……………………… 9分
(Ⅲ)f(an)=f(f(3n))=3×3n=3n+1,
an+1=f(3n+1)=f(f(an))=3an,a1=f(3)=6.
即数列{an}是以6为首项,以3为公比的等比数列.
∴an=6×3n.files/image243.gif) 1=2×3n(n=1,2,3…).………………………… 11分
1=2×3n(n=1,2,3…).………………………… 11分
于是.files/image248.gif) +
+.files/image250.gif) +…+
+…+.files/image252.gif) =
=.files/image018.gif) (
(.files/image053.gif) +
+.files/image256.gif) +…+
+…+.files/image258.gif) )=
)=.files/image018.gif) ×
×.files/image260.gif) .
.
显然.files/image067.gif) (
(.files/image263.gif) )<
)<.files/image067.gif) .………………………………………………12分
.………………………………………………12分
另一方面3n=(1+2)n=1+.files/image265.gif) ×2+
×2+.files/image267.gif) ×22+…+
×22+…+.files/image269.gif) ×2n≥1+2n,
×2n≥1+2n,
从而.files/image067.gif) (1
(1.files/image243.gif)
.files/image258.gif) )≥
)≥.files/image067.gif) (1
(1.files/image243.gif)
.files/image041.gif) )=
)=.files/image083.gif) .
.
综上得.files/image276.gif) ≤
≤.files/image248.gif) +
+.files/image250.gif) +…+
+…+.files/image250.gif) <
<.files/image067.gif) .………………………………14分
.………………………………14分
说明:其他正确解法按相应步骤给分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com