
题目列表(包括答案和解析)
已知数列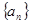 的各项均为正数,前
的各项均为正数,前 项和为
项和为 ,且
,且
(1)求证数列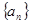 是等差数列;
是等差数列;
(2)设 …
…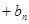 ,求
,求 。
。
【解析】(1) ,
, 当
当 时,
时,
当 时,由
时,由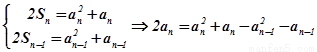 (3’)
(3’)
即 ,
,
所以数列 是等差数列
(6’)
是等差数列
(6’)
(2)由(1)可得 (8’)
(8’) (10’)
(10’)

已知过点 的动直线
的动直线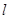 与抛物线
与抛物线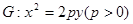 相交于
相交于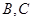 两点.当直线
两点.当直线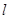 的斜率是
的斜率是 时,
时, .
.
(1)求抛物线 的方程;
的方程;
(2)设线段 的中垂线在
的中垂线在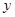 轴上的截距为
轴上的截距为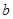 ,求
,求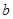 的取值范围.
的取值范围.
【解析】(1)B ,C
,C ,当直线
,当直线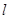 的斜率是
的斜率是 时,
时,
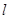 的方程为
的方程为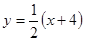 ,即
,即 (1’)
(1’)
联立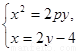 得
得 ,
,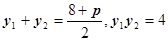 (3’)
(3’)
由已知  ,
,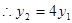 (4’)
(4’)
由韦达定理可得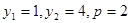 G方程为
G方程为 (5’)
(5’)
(2)设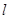 :
: ,BC中点坐标为
,BC中点坐标为 (6’)
(6’)
 得
得 由
由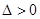 得
得 (8’)
(8’)

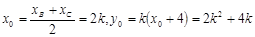
BC中垂线为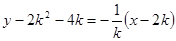 (10’)
(10’)

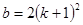 (11’)
(11’)

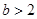
| AB |
| a2+λb2 |
| 1+λ |
| a+λb |
| 1+λ |
| log2010a+log2010b |
| 1+λ |
| a+λb |
| 1+λ |
| log2010a+log2010b |
| 1+λ |
| a+λb |
| 1+λ |
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com