
题目列表(包括答案和解析)
设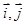 是直角坐标系中,x轴、y轴正方向上的单位向量,设
是直角坐标系中,x轴、y轴正方向上的单位向量,设

(1)若( ,求
,求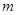 .
.
(2)若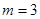 时,求
时,求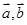 的夹角
的夹角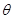 的余弦值.
的余弦值.
(3)是否存在实数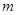 ,使
,使 ,若存在求出
,若存在求出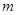 的值,不存在说明理由.
的值,不存在说明理由.
【解析】第一问中,利用向量的数量积为0,解得为m=-2
第二问中,利用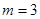 时,结合向量
时,结合向量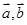 的夹角
的夹角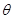 的余弦值公式解得
的余弦值公式解得
第三问中,利用向量共线,求解得到m不存在。
(1)因为设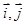 是直角坐标系中,x轴、y轴正方向上的单位向量,设
是直角坐标系中,x轴、y轴正方向上的单位向量,设


(2)因為
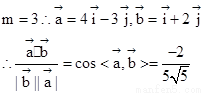
即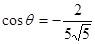 ;
;
(3)假設存在实数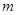 ,使
,使 ,則有
,則有
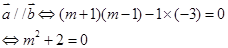
因此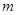 不存在;
不存在;
A.如果变量η与ξ之间存在着线性相关关系,则我们根据实验数据得到的点(xi,yi)(i=1,2, …,n)将散布在某一条直线的附近
B.如果两个变量η与ξ之间不存在着线性相关关系,那么根据它们的一组数据(xi,yi)(i=1,2, …,n)不能写出一个线性方程
C.设x,y是具有相关关系的两个变量,且x关于y的线性回归方程为![]() =bx+a,b叫做回归系数
=bx+a,b叫做回归系数
D.为使求出的线性回归方程有意义,可用统计假设检验的方法来判定变量η与ξ之间是否存在线性相关关系
已知函数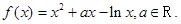
(Ⅰ)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(Ⅱ)令g(x)= f(x)-x2,是否存在实数a,当x∈(0,e](e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由;
(Ⅲ)当x∈(0,e]时,证明:
【解析】本试题主要是考查了导数在研究函数中的运用。第一问中利用函数f(x)在[1,2]上是减函数,的导函数恒小于等于零,然后分离参数求解得到a的取值范围。第二问中,
假设存在实数a,使 有最小值3,利用
有最小值3,利用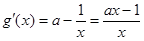 ,对a分类讨论,进行求解得到a的值。
,对a分类讨论,进行求解得到a的值。
第三问中,
因为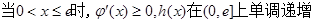 ,这样利用单调性证明得到不等式成立。
,这样利用单调性证明得到不等式成立。
解:(Ⅰ) 
(Ⅱ) 
(Ⅲ)见解析
已知真命题:“函数 的图像关于点
的图像关于点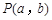 成中心对称图形”的充要条件为“函数
成中心对称图形”的充要条件为“函数 是奇函数”.
是奇函数”.
(Ⅰ)将函数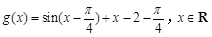 的图像向左平移
的图像向左平移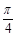 个单位,再向上平移2个单位,求此时图像对应的函数解析式,并利用题设中的真命题求函数
个单位,再向上平移2个单位,求此时图像对应的函数解析式,并利用题设中的真命题求函数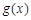 图像对称中心的坐标;
图像对称中心的坐标;
(Ⅱ)求函数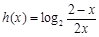 图像对称中心的坐标;
图像对称中心的坐标;
(Ⅲ)已知命题:“函数  的图像关于某直线成轴对称图像”的充要条件为“存在实数
的图像关于某直线成轴对称图像”的充要条件为“存在实数 和
和 ,使得函数
,使得函数 是偶函数”.判断该命题的真假,如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
是偶函数”.判断该命题的真假,如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com