
题目列表(包括答案和解析)
为了解某班关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| | 关注NBA | 不关注NBA | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
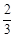 .
.| P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
| K | 2.706 | 3.841 | 60635 | 7.879 |
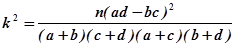 )其中n=a+b+c+d
)其中n=a+b+c+d为了解某班关注NBA是否与性别有关,对本班48人进行了问卷调查得到如下的列联表:
| 关注NBA | 不关注NBA | 合计 |
男生 |
| 6 |
|
女生 | 10 |
|
|
合计 |
|
| 48 |
已知在全班48人中随机抽取1人,抽到关注NBA的学生的概率为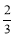 .
.
(1)请将上面的表补充完整(不用写计算过程),并判断是否有95%的把握认为关注NBA与性别有关?说明你的理由.
(2)现记不关注NBA的6名男生中某两人为a,b,关注NBA的10名女生中某3人为c,d,e,从这5人中选取2人进行调查,求:至少有一人不关注NBA的被选取的概率。
下面的临界值表,供参考
P(K2≥k) | 0.10 | 0.05 | 0.010 | 0.005 |
K | 2.706 | 3.841 | 60635 | 7.879 |
(参考公式: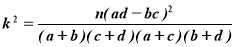 )其中n=a+b+c+d
)其中n=a+b+c+d
(12分)已知函数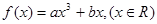 ,k*s*5u
,k*s*5u
(1)若函数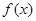 的图像在
的图像在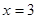 点处的切线与直线
点处的切线与直线 平行,且在
平行,且在 处取得极值,求
处取得极值,求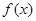 的解析式,并确定
的解析式,并确定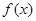 的单调递减区间。
的单调递减区间。
(2)若 时,函数
时,函数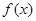 在
在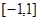 上是减函数,求b的取值范围。
上是减函数,求b的取值范围。
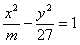 ,有如下信息:联立方程组
,有如下信息:联立方程组 消去y后得到方程Ax2+Bx+C=0,
消去y后得到方程Ax2+Bx+C=0,已知函数 ,
,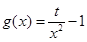 ,k为非零实数.
,k为非零实数.
(Ⅰ)设t=k2,若函数f(x),g(x)在区间(0,+∞)上单调性相同,求k的取值范围;
(Ⅱ)是否存在正实数k,都能找到t∈[1,2],使得关于x的方程f(x)=g(x)在[1,5]上有且仅有一个实数根,且在[-5,-1]上至多有一个实数根.若存在,请求出所有k的值的集合;若不存在,请说明理由.
【解析】本试题考查了运用导数来研究函数的单调性,并求解参数的取值范围。与此同时还能对于方程解的问题,转化为图像与图像的交点问题来长处理的数学思想的运用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com