甲.乙两人各射击一次.击中目标的概率分别是和.假设两人射击是否击中目标.相互之间没有影响,每次射击是否击中目标.相互之间没有影响. (Ⅰ)求甲射击4次.至少1次未击中目标的概率, (Ⅱ)求两人各射击4次.甲恰好击中目标2次且乙恰好击中目标3次的概率, (Ⅲ)假设两人连续两次未击中目标.则停止射击.问:乙恰好射击5次后.被中止射击的概率是多少? 解:(Ⅰ)记“甲连续射击4次.至少1次未击中目标 为事件A1.由题意.射击4次.相当于4次独立重复试验.故P(A1)=1- P()=1-=. 答:甲射击4次.至少1次未击中目标的概率为, (Ⅱ) 记“甲射击4次.恰好击中目标2次 为事件A2.“乙射击4次.恰好击中目标3次 为事件B2.则 .. 由于甲.乙设计相互独立.故. 答:两人各射击4次.甲恰好击中目标2次且乙恰好击中目标3次的概率为, (Ⅲ)记“乙恰好射击5次后.被中止射击 为事件A3.“乙第i次射击为击中 为事件Di..则A3=D5D4.且P(Di)=.由于各事件相互独立.故P(A3)= P(D5)P(D4)P()=×××(1-×)=. 答:乙恰好射击5次后.被中止射击的概率是. [探索题]甲.乙.丙三台机床各自独立地加工同一种零件.已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为.乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为.甲.丙两台机床加工的零件都是一等品的概率为. (1)分别求甲.乙.丙三台机床各自加工的零件是一等品的概率, (2)从甲.乙.丙加工的零件中各取一个检验.求至少有一个一等品的概率. 解:(1)设A.B.C分别为甲.乙.丙三台机床各自加工的零件是一等品的事件. 由题设条件有: ① ② ③ 即 由①③得P(B)=1-P(C). 代入②得27[P(C)]2-51P(C)+22=0. 解得P(C)=或. 将P(C)=分别代入③②可得P(A)=.P(B)=. 即甲.乙.丙三台机床各自加工的零件是一等品的概率分别是... (2)记D为从甲.乙.丙加工的零件中各取一个检验至少有一个一等品的事件.则 P(D)=1-P()=1-[1-P(A)][1-P(B)][1-P(C)]=1-··=. 故从甲.乙.丙加工的零件中各取一个检验.至少有一个一等品的概率为. 备选题: 【
查看更多】
题目列表(包括答案和解析)
(2005
江苏,20)甲、乙两人各射击1次,击中目标的概率分别是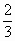 和
和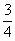 .假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
(1)
求甲射击4次,至少有1次未击中目标的概率;
(2)
求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)
假设某人连续2次未击中目标,则中止其射击.问:乙恰好射击5次后,被中止射击的概率是多少?
查看答案和解析>>

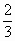 和
和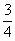 .假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.