
题目列表(包括答案和解析)
| 特殊函数 | 抽象函数 | ||
f(x)=xα f(x)=xα |
f(xy)=f(x)f(y) | ||
f(x)=ax(a>0且a≠1) f(x)=ax(a>0且a≠1) |
f(x+y)=f(x)f(y) | ||
f(x)=logax(a>0且a≠1) f(x)=logax(a>0且a≠1) |
f(xy)=f(x)+f(y) | ||
f(x)=tanx f(x)=tanx |
f(x+y)=
|
抽象函数所恒满足的条件通常是以具体函数为蓝本归纳出来的,比如:若函数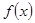
对于任意的 ,恒满足
,恒满足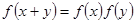 ,那么函数
,那么函数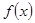 可以以
可以以 作为蓝本.
作为蓝本.
若函数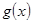 对于任意的
对于任意的 ,恒满足
,恒满足 ,则函数
,则函数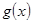 可以以函
可以以函
数__________作为蓝本.
已知函数![]() 的定义域为
的定义域为![]() 且
且![]() ,对任意
,对任意![]() 都有
都有![]()
![]()
数列![]() 满足
满足![]() N
N![]() .证明函数
.证明函数![]() 是奇函数;求数列
是奇函数;求数列![]() 的通项公式;令
的通项公式;令![]() N
N![]() , 证明:当
, 证明:当![]() 时,
时,![]() .
.
(本小题主要考查函数、数列、不等式等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com