
题目列表(包括答案和解析)
 【倾听理解】(这是一次数学活动课上,师生利用“几何画板”软件探究函数性质的活动片段)
【倾听理解】(这是一次数学活动课上,师生利用“几何画板”软件探究函数性质的活动片段)| 2 |
| x |
| 3 |
| x |
| MN |
| PM |
| 1 |
| 2 |
(1)夜晚,小明在路灯下散步.已知小明身高1.5米,路灯的灯柱高4.5米.
①如图1,若小明在相距10米的两路灯AB、CD之间行走(不含两端),他前后的两个影子长分别为FM=x米,FN=y米,试求y与x之间的函数关系式,并指出自变量x的取值范围;
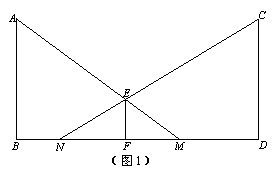
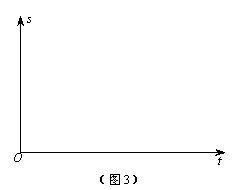
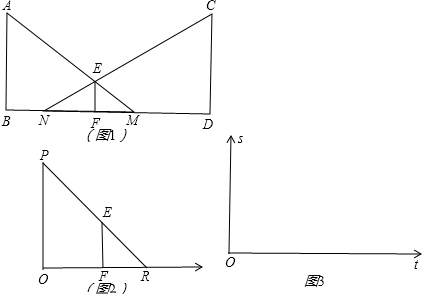
②有言道:形影不离.其原意为:人的影子与自己紧密相伴,无法分离.但在灯光下,人的速度与影子的速度却不是一样的!如图2,若小明在灯柱PQ前,朝着影子的方向(如图箭头),以0.8米/秒的速度匀速行走,试求他影子的顶端R在地面上移动的速度.

(2)我们知道,函数图象能直观地刻画因变量与自变量之间的变化关系.相信,大家都听说过龟兔赛跑的故事吧.现有一新版龟兔赛跑的故事:由于兔子上次比赛过后不服气,于是单挑乌龟再来另一场比赛,不过这次路线由乌龟确定……比赛开始,在同一起点出发,按照规定路线,兔子飞驰而出,极速奔跑,直至跑到一条小河边,遥望着河对岸的终点,兔子呆坐在那里,一时不知怎么办.过了许久,乌龟一路跚跚而来,跳入河中,以比在陆地上更快的速度游到对岸,抵达终点,再次获胜.根据新版龟兔赛跑的故事情节,请在同一坐标系内(如图3),画出乌龟、兔子离开终点的距离s与出发时间t的函数图象示意图.(实线表示乌龟,虚线表示兔子)

在-次数学活动课上,老师出了-道题:
(1)解方程x2-2x-3=0.
巡视后老师发现同学们解此题的方法有公式法、配方法和十字相乘法(分解因式法)。
接着,老师请大家用自己熟悉的方法解第二道题:
(2)解关于x的方程mx2+(m一3)x一3=0(m为常数,且m≠0).
老师继续巡视,及时观察、点拨大家.再接着,老师将第二道题变式为第三道题:
(3)已知关于x的函数y=mx2+(m-3)x-3(m为常数).
①求证:不论m为何值,此函数的图象恒过x轴、y轴上的两个定点(设x轴上的定点为A,y轴上的定点为C);
②若m≠0时,设此函数的图象与x轴的另一个交点为反B,当△ABC为锐角三角形时,求m的取值范围;当△ABC为钝角三角形时,观察图象,直接写出m的取值范围.
请你也用自己熟悉的方法解上述三道题.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com