
题目列表(包括答案和解析)
如图所示,竖直放置的平行金属导轨上端跨接一个阻值为R的电阻。质量为m的金属棒MN可沿平行导轨竖直下滑,不计轨道与金属棒的电阻。金属棒自由下落了 h后进入一个有上下边界的匀强磁场区域,磁场方向垂直轨道平面,磁场宽度也为h ,设金属棒MN到达上边界aa'时的速度为 ,到达下边界bb'时的速度为
,到达下边界bb'时的速度为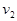 ,则以下说法正确的是
,则以下说法正确的是
A.进入磁场区后,MN可能做匀速运动,则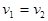 |
B.进入磁场区后,MN可能做加速运动,则 |
C.进入磁场区后,MN可能做减速运动,则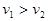 |
D.通过磁场区域的过程中,R上释放出的焦耳热一定是mg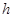 |
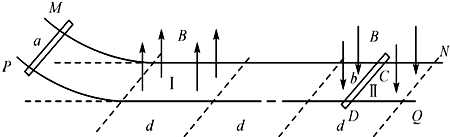
如图所示,两根间距为L的金属导轨MN和PQ,电阻不计,左端弯曲部分光滑,水平部分导轨与导体棒间的滑动摩擦因数为μ,水平导轨左端有宽度为d、方向竖直向上的匀强磁场Ⅰ,右端有另一磁场Ⅱ,其宽度也为d,但方向竖直向下,两磁场的磁感强度大小均为B0,相隔的距离也为d.有两根质量为m、电阻均为R的金属棒a和b与导轨垂直放置,b棒置于磁场Ⅱ中点C、D处.现将a棒从弯曲导轨上某一高处由静止释放并沿导轨运动下去.
(1)当a棒在磁场Ⅰ中运动时,若要使b棒在导轨上保持静止,则a棒刚释放时的高度应小于某一值h0,求h0的大小;
(2)若将a棒从弯曲导轨上高度为h(h<h0)处由静止释放,a棒恰好能运动到磁场Ⅱ
的左边界处停止,求a棒克服安培力所做的功;
(3)若将a棒仍从弯曲导轨上高度为h(h<h0)处由静止释放,为使a棒通过磁场Ⅰ时恰好无感应电流,可让磁场Ⅱ的磁感应强度随时间而变化,将a棒刚进入磁场Ⅰ的时刻记为t=0,此时磁场Ⅱ的磁感应强度为B0,试求出在a棒通过磁场Ⅰ的这段时间里,磁场Ⅱ的磁感应强度随时间变化的关系式.
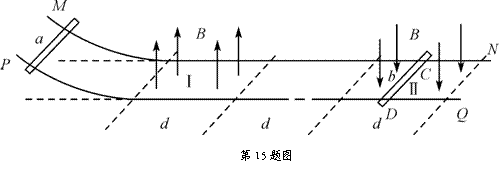 |
如图所示,两根间距为L的金属导轨MN和PQ,电阻不计,左端弯曲部分光滑,水平部分导轨与导体棒间的滑动摩擦因数为μ,水平导轨左端有宽度为d、方向竖直向上的匀强磁场Ⅰ,右端有另一磁场Ⅱ,其宽度也为d,但方向竖直向下,两磁场的磁感强度大小均为B0,相隔的距离也为d.有两根质量为m、电阻均为R的金属棒a和b与导轨垂直放置,b棒置于磁场Ⅱ中点C、D处.现将a棒从弯曲导轨上某一高处由静止释放并沿导轨运动下去.
(1)当a棒在磁场Ⅰ中运动时,若要使b棒在导轨上保持静止,则a棒刚释放时的高度应小于某一值h0,求h0的大小;
(2)若将a棒从弯曲导轨上高度为h(h<h0)处由静止释放,a棒恰好能运动到磁场Ⅱ的左边界处停止,求a棒克服安培力所做的功;
(3)若将a棒仍从弯曲导轨上高度为h(h<h0)处由静止释放,为使a棒通过磁场Ⅰ时恰好无感应电流,可让磁场Ⅱ的磁感应强度随时间而变化,将a棒刚进入磁场Ⅰ的时刻记为t=0,此时磁场Ⅱ的磁感应强度为B0,试求出在a棒通过磁场Ⅰ的这段时间里,磁场Ⅱ的磁感应强度随时间变化的关系式。
如图所示,两根间距为L的金属导轨MN和PQ,电阻不计,左端弯曲部分光滑,水平部分导轨与导体棒间的滑动摩擦因数为μ,水平导轨左端有宽度为d、方向竖直向上的匀强磁场Ⅰ,右端有另一磁场Ⅱ,其宽度也为d,但方向竖直向下,两磁场的磁感强度大小均为B0,相隔的距离也为d.有两根质量为m、电阻均为R的金属棒a和b与导轨垂直放置,b棒置于磁场Ⅱ中点C、D处.现将a棒从弯曲导轨上某一高处由静止释放并沿导轨运动下去.
(1)当a棒在磁场Ⅰ中运动时,若要使b棒在导轨上保持静止,则a棒刚释放时的高度应小于某一值h0,求h0的大小;
(2)若将a棒从弯曲导轨上高度为h(h<h0)处由静止释放,a棒恰好能运动到磁场Ⅱ的左边界处停止,求a棒克服安培力所做的功;
(3)若将a棒仍从弯曲导轨上高度为h(h<h0)处由静止释放,为使a棒通过磁场Ⅰ时恰好无感应电流,可让磁场Ⅱ的磁感应强度随时间而变化,将a棒刚进入磁场Ⅰ的时刻记为t=0,此时磁场Ⅱ的磁感应强度为B0,试求出在a棒通过磁场Ⅰ的这段时间里,磁场Ⅱ的磁感应强度随时间变化的关系式。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com