
题目列表(包括答案和解析)
(本小题满分12分) 已知椭圆![]() 的离心率
的离心率![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切。(I)求a与b;(II)设椭圆的左,右焦点分别是F1和F2,直线
相切。(I)求a与b;(II)设椭圆的左,右焦点分别是F1和F2,直线![]() 且与x轴垂直,动直线
且与x轴垂直,动直线![]() 轴垂直,
轴垂直,![]() 于点P,求线段PF1的垂直平分线与
于点P,求线段PF1的垂直平分线与![]() 的交点M的轨迹方程,并指明曲线类型。
的交点M的轨迹方程,并指明曲线类型。
(本小题满分12分)
已知抛物线以原点为顶点,以![]() 轴为对称轴,焦点在直线
轴为对称轴,焦点在直线![]() 上.
上.
(1)求抛物线的方程;(2)设![]() 是抛物线上一点,点
是抛物线上一点,点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的最小值(用
的最小值(用![]() 表示),并指出此时点
表示),并指出此时点![]() 的坐标。
的坐标。
(本小题满分12分)
如图,已知椭圆![]() 的离心率为
的离心率为![]() ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点![]() 为顶点的三角形的周长为
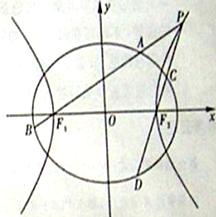
为顶点的三角形的周长为![]() .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设![]() 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线![]() 和
和![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 和
和![]() .
.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明
,证明![]() ;
;
(Ⅲ)是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)
如图,已知椭圆![]() 的离心率为
的离心率为![]() ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点![]() 为顶点的三角形的周长为
为顶点的三角形的周长为![]() .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设![]() 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线![]() 和
和![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 和
和![]() .
.

(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明
,证明![]() ;
;
(Ⅲ)是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)
如图,已知椭圆![]() 过点
过点![]() ,两个焦点分别为
,两个焦点分别为![]() ,
,![]() 为坐标原点,平行于
为坐标原点,平行于![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() ,
,
(Ⅰ)求椭圆![]() 的方程;
的方程;
 (Ⅱ)试问直线
(Ⅱ)试问直线![]() 的斜率之和是否为定值,若为定值,求出以线段
的斜率之和是否为定值,若为定值,求出以线段![]() 为直径且过点
为直径且过点![]() 的圆的方程;若不存在,说明理由.
的圆的方程;若不存在,说明理由.
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
C
C
B
B
C
C
A
C
B
B
二、填空题
13..files/image229.gif) 14.
14. .files/image231.gif) 15.
15. .files/image233.gif) 16.___-1__
16.___-1__
三、解答题
17.解:1) .files/image235.gif)
=.files/image237.gif)
.files/image239.gif)
.files/image241.gif)
.files/image243.gif)
.files/image245.gif)
2).files/image247.gif)
.files/image249.gif) 或
或.files/image251.gif)
.files/image253.gif) 或
或.files/image255.gif) ,而
,而.files/image257.gif)
.files/image259.gif)
.files/image261.gif) ,
,.files/image263.gif)
18.解:(I)由题意:.files/image265.gif) 的取值为1,3,又
的取值为1,3,又.files/image267.gif)
.files/image269.gif)
|