
题目列表(包括答案和解析)
例
( 2005全国卷III)已知函数![]() ,
,![]() (Ⅰ)求
(Ⅰ)求![]() 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设![]() ,函数
,函数![]() ,若对于任意
,若对于任意![]() ,总存在
,总存在![]() 使得
使得![]() 成立,求
成立,求![]() 的取值范围。
的取值范围。
()(2005 全国卷III)用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少?

【练】
(1)(2005全国卷1)已知椭圆的中心为坐标原点O,焦点在![]() 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,![]() 与
与![]() 共线。(Ⅰ)求椭圆的离心率;(Ⅱ)设M为椭圆上任意一点,且
共线。(Ⅰ)求椭圆的离心率;(Ⅱ)设M为椭圆上任意一点,且![]() ,证明
,证明![]() 为定值。
为定值。
(2005
全国III,16)已知在△ABC中,∠ACB=90°,BC=3,AC=4,P是AB上的点,则点P到AC、BC的距离乘积的最大值是________.(2005
全国Ⅰ,16)在正方体ABCD- 中,过对角线
中,过对角线 的一个平面交
的一个平面交 于E,交
于E,交 于F,则
于F,则
A.四边形
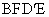 一定是平行四边形.
一定是平行四边形.
B.四边形
 有可能是正方形.
有可能是正方形.
C.四边形
 在底面ABCD内的投影一定是正方形.
在底面ABCD内的投影一定是正方形.
D.平面
 有可能垂直于平面
有可能垂直于平面 .
.
以上结论正确的为
________(按照原顺序写出所有正确结论的代号).湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com