
题目列表(包括答案和解析)
(07年天津卷文)(14分)
设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 是椭圆上的一点,
是椭圆上的一点,![]() ,原点
,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)证明![]() ;
;
(Ⅱ)求![]() 使得下述命题成立:设圆
使得下述命题成立:设圆![]() 上任意点
上任意点![]() 处的切线交椭圆于
处的切线交椭圆于![]() ,
,![]() 两点,则
两点,则![]() .
.
(07年天津卷理)(14分)
设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 是椭圆上的一点
是椭圆上的一点![]()
![]()
![]() 原点
原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(I)证明:![]() ;
;
(II)设![]() 为椭圆上的两个动点
为椭圆上的两个动点![]()
![]()
![]() 过原点
过原点![]() 作直线
作直线![]() 的垂线
的垂线![]() 垂足为
垂足为![]() 求点
求点![]() 的轨迹方程.
的轨迹方程.
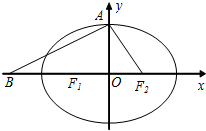 (2013•天津模拟)设椭圆C:
(2013•天津模拟)设椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| BF1 |
| F1F2 |
| 3 |
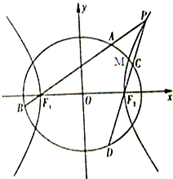 (2011•天津模拟)如图,椭圆
(2011•天津模拟)如图,椭圆
| ||
|
| ||
| b2 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com