
题目列表(包括答案和解析)
已知椭圆C:![]() 的离心率为
的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .
.
(1)求椭圆C的方程;
(2)设直线![]() 与椭圆C交于A、B两点,以
与椭圆C交于A、B两点,以![]() 弦为直径的圆过坐标原点
弦为直径的圆过坐标原点![]() ,试探讨点
,试探讨点![]() 到直线
到直线![]() 的距离是否为定值?若是,求出这个定值;若不是,说明理由.
的距离是否为定值?若是,求出这个定值;若不是,说明理由.
已知函数![]()
![]() .
.
(1)讨论函数![]() 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数![]() 在
在![]() 处取得极值,对
处取得极值,对![]()
![]() ,
,![]() 恒成立,
恒成立,
求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,求证:
时,求证:![]() .
.
 已知幂函数y=f(x)的图象经过点(2,4),对于偶函数y=g(x)(x∈R),当x≥0时,g(x)=f(x)-2x.
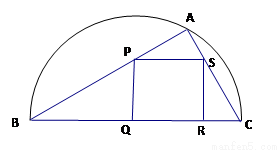
已知幂函数y=f(x)的图象经过点(2,4),对于偶函数y=g(x)(x∈R),当x≥0时,g(x)=f(x)-2x.如图,某小区准备绿化一块直径为 的半圆形空地,
的半圆形空地,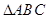 外的地方种草,
外的地方种草,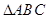 的内接正方形
的内接正方形 为一水池,其余地方种花.若
为一水池,其余地方种花.若
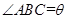 ,设
,设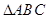 的面积为
的面积为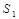 ,正方形
,正方形 的面积为
的面积为 ,将比值
,将比值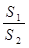 称为“规划合理度”.
称为“规划合理度”.
(1)试用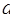 ,
, 表示
表示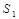 和
和 .
.
(2)当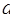 为定值,
为定值, 变化时,求“规划合理度”取得最小值时的角
变化时,求“规划合理度”取得最小值时的角 的大小.
的大小.
【解析】第一问中利用在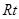
 ABC中
ABC中  ,
,
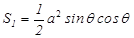 =
=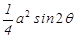 设正方形的边长为
设正方形的边长为 则
则 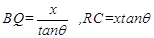
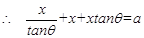 然后解得
然后解得
第二问中,利用 而
而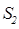 =
=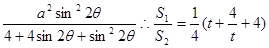
借助于  为减函数
得到结论。
为减函数
得到结论。
(1)、 如图,在
 ABC中
ABC中  ,
,
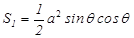 =
=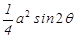
设正方形的边长为 则
则 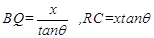
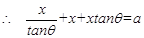
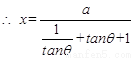 =
=
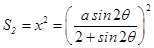
(2)、 而
而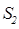 =
=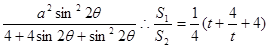 ∵0 <
∵0 <  <
<
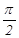 ,又0 <2
,又0 <2 <
<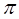 ,
,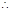 0<t£1
0<t£1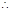
 为减函数
为减函数
当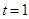 时
时 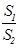 取得最小值为
取得最小值为 此时
此时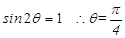
本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
某生产旅游纪念品的工厂,拟在2010年度将进行系列促销活动.经市场调查和测算,该纪念品的年销售量x万件与年促销费用t万元之间满足3-x与t+1成反比例.若不搞促销活动,纪念品的年销售量只有1万件.已知工厂2010年生产纪念品的固定投资为3万元,每生产1万件纪念品另外需要投资32万元.当工厂把每件纪念品的售价定为:“年平均每件生产成本的150%”与“年平均每件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)
(1)求出x与t所满足的关系式;
(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;
(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com